【最优化】梯度下降算法及其变体总结
注:本文的成文时间比本站最优化理论相关的文章更早🎢,文章风格也尽量是从没有相关理论基础的视角出发的,并不涉及相关数学证明💯。总体可作为独立文章观看🔔。
基本思想及原始版本
对于一个无约束的最优化问题:,其中 为 上具有一节连续偏导数的函数。
为求得函数 的最小值,以及最优解 ,最主要的方法可以分为两大类:最优条件法和迭代法。
最优条件法 是指当函数存在解析形式时,我们可以利用最优性条件解出其显式最优解。比如,当 在其理论最小值点 处可微时,我们有:
即各项偏导数为零。
但是在实际中,求解这样的方程往往十分困难。这就引出了第二大类方法:迭代法。
关于更多最优性条件知识详见本站文章:
迭代法中,又以梯度下降法(Gradient Descent) 较为经典,它是一种常用的一阶(first-order)优化方法,是求解无约束优化问题最简单、最经典的方法之一。
其核心思想用到了数学中梯度的几何意义:梯度方向是函数值变化最快的方向。其正方向是增加最快的方向,反方向则是减小最快的方向。
因此,梯度下降法采用一种逐步往函数值更低的方向更新 的取值的方式,不断迭代以得到最优(近似)解。如下图所示:
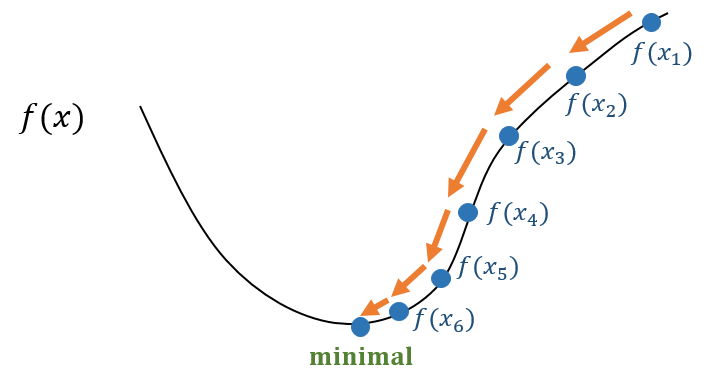
形式化来说,首先需要设定初始点,然后不断更新 进行迭代,使得,当结果收敛,即 时,迭代结束。
最原始的更新方法就是根据梯度的几何意义,取. 其中, 为学习率,它决定了点的移动步长; 为计算精度,决定了迭代的结束条件。
必备条件:函数 必须可微,即梯度 必须存在
优点:实现简单
缺点:梯度下降法一阶收敛,往往需要多次迭代才能接近问题最优解
学习率的确定:
当 的解析解不存在或难以求解时,我们通常需要使用 一维搜索 来搜索最优的学习率。一维搜索是一些数值方法,有0.618法、Fibonacci法、抛物线法等等,详见本站文章:
在实际使用中,为了简便,也可以使用一个预定的常数而不用一维搜索来确定学习率。这时的选择往往根据经验或者通过试算来确定的。学习率过小则收敛慢,学习率过大可能震荡而不收敛。
批量梯度下降法 |BGD
批量梯度下降法(Batch Gradient Descent, BGD)是梯度下降法的最原始的形式,其特点就是每一次训练迭代都需要利用所有的训练样本。
对于机器学习/深度学习任务来说,我们需要优化的目标函数往往是损失函数,而损失函数中要涉及到所有的训练样本(特别是监督学习)。
以线性回归为例,对于第 个样本,有:
为待学习的参数。为了求出参数,我们定义损失函数:
J(\theta_0, \theta_1) = \frac{1}{2n} \sum_ \limits {i=1}^{n}(h_{\theta}(x_i) - y_i)^2因此,如果对参数 求偏导,就有:
\frac{\partial J(\theta_0,\theta_1)}{\partial \theta_1} = \frac{1}{n} \sum_ \limits {i=1}^{n} (h_{\theta}(x_i)-y_i)\cdot x_i我们的目的就是对 迭代更新,而每次迭代时,从上式可以看出,我们都需要对所有样本进行求和操作,由全数据集确定的方向能够更好地代表样本总体,从而更准确地朝向极值所在的方向。当目标函数为凸函数时,BGD一定能够得到全局最优。
但是,这也极大增加了BGD的求解效率。
随机梯度下降法 |SGD
随机梯度下降算法(Stochastic gradient descent,SGD)为了解决 BGD 的大样本问题,提出了每次迭代都选择一个 「训练样本对」: ,仅对这个「样本对」对应的样本损失函数 求偏导。
同样以前述损失函数 为例,它可以看作每一个样本的损失函数的平均:
因此,在某次更新时,我们随机选择了其中一个「训练样本对」: ,作更新:
显然,随机梯度下降迭代过程中,考虑的下降方向并不是全局下降方向,而是使得某个随机选中的样本的损失函数下降的方向。在一步迭代中,这种局部样本的下降未必会导致全局损失的下降,但是当迭代次数足够的时候,绝大部分样本都会被考虑到,最终一步一步走向全局最优解。
注意,在使用SGD时,需要对样本进行随机化处理。
小批量梯度下降法 |MBGD
经典梯度下降虽然稳定性比较强,但是大样本情况下迭代速度较慢;
随机梯度下降虽然每一步迭代计算较快,但是其稳定性不太好;
所以,为了协调稳定性和速度,小批量梯度下降(Mini-Batch Gradient Descent,MBGD)应运而生。
小批量梯度下降是从 个样本中随机且不重复地选择 /batch_size个进行样本损失函数的平均。
这个方法在深度学习的网络训练中有着广泛地应用,因为其既有较高的精度,也有较快的训练速度。
Momentum |动量
SGD (此处指上述三种GD方法)具有收敛不稳定性:在 SGD 中,参数 的迭代变化量都只是与当前梯度正相关,这会导致在迭代过程中, 在最优解附近以较大幅度震荡从而无法收敛。
Momentum 能在一定程度上缓解 SGD 收敛不稳定的问题,它的思想就是模拟物体运动的惯性:当我们跑步时转弯,我们最终的前进方向是由我们之前的方向和转弯的方向共同决定的。
Momentum 在每次更新时,保留一部分上次的更新方向:
即通过引入动量系数 表示保留原来方向的程度 ,通常设置为0.9左右。
优点
- 由于在迭代时考虑了上一次 的迭代变化量,所以在最优解附近通常具有梯度因方向相反而抵消的效果,从而在一定程度上缓解 SGD 的收敛不稳定问题;
- 除此之外,Momentum 还具有一定的摆脱局部最优的能力,如果上一次梯度较大,而当前梯度为0时,仍可能按照上次迭代的方向冲出局部最优点。
缺点:又增加了额外的超参数 需要设置,它的选取同样会影响到结果.
NAG |Nesterov Accelerated Gradient
Nesterov Momentum 又叫做 Nesterov Accelerated Gradient(NAG) ,是基于 Momentum 的加速算法.
NAG认为:既然都把上一次迭代的结果作为本次预期的指标之一了,就应该预期到底,将当前梯度替换原本应该预期的梯度,具体表示如下:
式中的 表示,按照原 Momentum 算法得到的本次更新 作为“原本的迭代结果”,我对其求梯度得到更有可能的方向指导,并纳入真正的本次更新中。
AdaGrad
AdaGrad 即 Adaptive Gradient ,自适应梯度法。它自适应地为各个参数分配不同的学习率:对于收敛贡献度小的参数可以进行大幅度的调整,对于收敛贡献大参数则进行小幅度的微调,因而适用于处理稀疏数据。
对了公式的简练,此后我们用 表示第 次更新所得到的参数 对目标函数的梯度,用 表示梯度向量的各项元素自平方,即.
则 AdaGrad 定义第 次迭代的学习率如下:
需要实现给定一个固定的初始学习率因子。
优点:解决了 SGD 中学习率不能自适应调整的问题
缺点:学习率单调递减,在迭代后期可能导致学习率变得特别小而导致收敛及其缓慢
AdaDelta/RMSprop
AdaDelta 是在 Adagrad 提出的后一年提出,它解决了 Adagrad 面临的两个问题,即迭代后期可能导致学习率变得特别小而导致收敛及其缓慢的问题,以及初始学习率需要人为设定的问题。
在 AdaGrad 的实际算法中,可以通过中间变量 来对此前的梯度进行累计,即每一次迭代都可以通过 实现。而 AdaDelta 主要是在这个累计过程中引入参数 实现用梯度平方的指数加权平均代替了至今全部梯度的平方和,避免了后期更新时更新幅度逐渐趋近于0的问题。
其中,.
也可以如下表示:
定义第 次迭代的中间变量 ,新的均方根就表示为:
RMSprop 方法则是之间做如下更新:
其中每次的增量也就是 。
AdaDelta 方法在此基础上,尝试利用增量 的信息,通过对其也做一个累加贡献计算:
将其作为动态的因子替换原本的初始学习率,从而有第 次迭代的增量:
Adam|Adaptive Moment Estimation
Adam 是 Momentum 和 AdaDelta 的结合体,将梯度的方向信息 和学习率的累计 都运用了起来。
事实上,他们都可以用前面的符号 来表示,分别表示 的一阶矩和二阶矩估计 .
此外,Adam为了解决衰减率(decay rate)很小时矩估计结果最终都会趋于0的问题,对其进行校正:
最终得到:
优点:结合 Momentum 和 Adagrad,稳定性好,收敛速度很快。同时相比于 Adagrad ,不用存储全局所有的梯度,适合处理大规模数据。有一说是Adam是世界上最好的优化算法,无脑用它就对了。
缺点:收敛速度虽快,但实际运用时往往没有 SGD 的解更优 ,因为进入局部最小值之后会反复在局部最小值附近抖动。
附录:PyTorch中的优化器
待更: