拓扑排序、最短路径、二部图、最大团| 算法之于图

拓扑排序|_{Topological sorting}

有向无环图

有向无环图 Directed Acyclic Graph，缩写 DAG。顾名思义，是有向图中没有环的图。

DAG的性质与判定

DAG 的性质：

1. 能拓扑排序的图，一定是有向无环图；
   • 如果有环，那么环上的任意两个结点在任意序列中都不能拓扑排序。
2. 有向无环图，一定能拓扑排序；
   （归纳法证明）假设结点数不超过 $k$ 的 有向无环图都能拓扑排序，那么对于结点数等于 $k$ 的，考虑执行拓扑排序第一步之后的情形即可。

DAG 的判定：
根据 DAG 的性质，可以直接得到这样的结论：检验它是否可以进行 拓扑排序 即可。

当然也有另外的方法，可以对图进行一遍DFS，在得到的 DFS 树上看看有没有连向祖先的非树边（返祖边）。如果有的话，则有环。

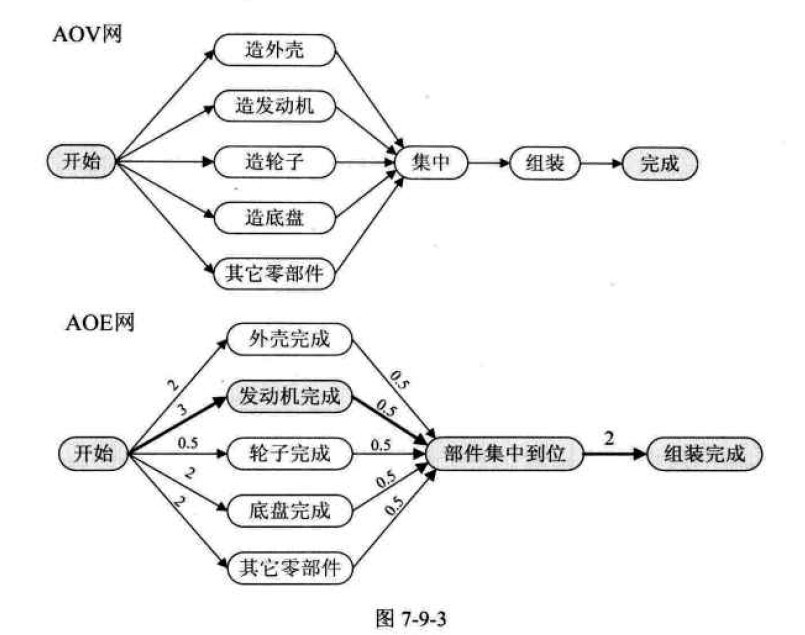
AOV网

某个工程或者某种流程可以分为若干个小的工程或阶段，这些小的工程或阶段就称为活动(Activity)。若以图中的顶点表示活动，有向边表示活动之间的优先关系，如 弧$<V_i,V_j>$ 表示活动$V_i$ 必须先于$V_j$ 完成，则这样的有向图称为 AOV 网（Activity On Vertex Network）。

我们称$V_i$ 是$V_j$ 的紧前工作，也就是其直接前驱；$V_j$ 是$V_i$ 的紧后工作，也就是直接后继。

• 前驱活动：有向边起点的活动被称为终点的前驱活动，即只有当这个活动的前驱活动都完成之后，才可以开始该活动；
• 后继活动：有向边终点的活动被称为起点的后继活动。

显然，AOV 网 本质是 DAG

拓扑排序

从图论的角度定义。对一个有向无环图 DAG :$G$ 进行拓扑排序，就是将$G$ 中所有顶点排成一个线性序列，使得图中任意一对顶点$u$ 和$v$ ，若边$e=<u,v>\in E(G)$，则顶点$u$ 在线性序列中排列在顶点$v$ 之前。
通常，这样的线性序列称为满足拓扑次序 (Topological Order) 的序列，简称拓扑序列。

值得注意的是，拓扑排序不一定唯一。

从离散数学的角度定义。假设$(A,≤)$ 是有限偏序集，对其进行拓扑排序是指将其扩展成一个全序集$(A,\prec)$，使得$\leq\subseteq\prec$ ，即对$\forall a,b\in A$，若$a≤b$，则$a\prec b$。

将拓扑排序用于 AOV 网中，即是将 AOV 网中所有活动排成一个序列，使得每个活动的前驱活动都排在该活动的前面。可以说，拓扑排序主要是为解决一个工程能否有序地顺利进行。

求解 DAG/AOV 的拓扑排序，常用的算法是 Kahn 算法。

Kahn算法

Kahn 算法 也叫入度表算法。
根据拓扑排序的定义，我们自然想到整张 DAG 中没有入度的结点就是拓扑序列中的第一个结点。换句话说，在AOV网中没有任何直接前驱的工作，就是应当完成的第一项工作。

而 Kahn算法的关键就在于需要维护一个入度为0的顶点的集合，记为$S$：

每次从$S$ 中取出一个点$u$ 放入最终用于存放序列结果的表（记为$L$）中。 然后将与$u$ 相关的的所有边都在图中进行删除，如$<u, v_1>, <u, v_2>, <u, v_3> \cdots$

删除过程中，若某条边$<u, v>$删除后，与$u$ 相邻的点$v$ 的入度变为$0$，则将$v$ 放入$S$ 中。

不断重复以上过程，直到集合$S$ 为空。
检查图中是否仍然存在边，如果有，那么这个图一定有环路，否则返回$L$，$L$ 中顶点的顺序就是拓扑序列结果。

可以发现，Kahn算法属于一种 BFS 算法。

一个拓扑排序的示例如下：

Kahn 算法的伪代码如下：

$$\begin{aligned} &\text{Algorithm: }\;\text{Kahn-Topo}(G)\\\\ 1.&\;L\leftarrow\varnothing\\ 2.&\;S\leftarrow\text{当前图 }G\text{ 中所有入度为 0 的顶点}\\ 3.&\;\mathbf{while}\;S\neq\varnothing\;\mathbf{do}\\ 4.&\;\qquad v\leftarrow S.\text{pop}()\;//\text{从 }S\text{ 中弹出一个顶点}\\ 5.&\;\qquad L\leftarrow L\cup\{v\}\;//\text{加入表 }L\\ 6.&\;\qquad\mathbf{for\; each\;} e=\text{<}x,y\text{>}\in E(G)\;\mathbf{do}\\ 7.&\;\qquad\qquad \mathbf{if}\;v= x\;\mathbf{then}\\ 8.&\;\qquad\qquad\qquad \text{delete }e\text{ from }G\\ 9.&\;\qquad\qquad \mathbf{if}\;\text{no other Edge }e'\in E(G) \text{ make } e'=<*,y>\;\mathbf{then}\\ 10.&\;\qquad\qquad\qquad S\leftarrow S\cup\{y\}\\ 11.&\;\mathbf{if}\;E(G)=\varnothing\;\mathbf{then\;return}\; L\\ 12.&\;\mathbf{else}\;\mathbf{return}\; error \end{aligned}$$

假设该无环有向图$G = <V, E>$ 在初始化入度为$0$ 的集合$S$ 的时候就需要遍历整个图，并检查每一条边，因而有$O(|E|+|V|)$ 的复杂度。
然后对该集合进行操作，显然也是需要$O(|E|+|V|)$ 的时间复杂度。

因而总的时间复杂度就有$O(|E|+|V|)$，而在邻接矩阵下需要$O(|V|^2)$.

编程实现

template<class elementType> 
void ALGraph<elementType>::TopSort(elementType res[]){
    //有向图的拓扑排序 
    //结果存入 传入的res数组中
    int visited[MAXVEXMUN];//记忆是否访问过
    int flag = 1,idx = 0;
    memset(visited,0,this->VexNum+1);
    while(idx != this->VexNum){//从未访问过的结点中查询入度为0的结点下标
        for(int i = 0; i < this->VexNum && visited[i] == 0; i++){
            for(int j = 0; j < this->VexNum && visited[j] == 0; j++){
                ArcNode* temp = this->GraphList[j].firstarc;
                while(temp){//循环法遍历链表
                    if(temp->VexIndex == i){flag = 0;break;}
                    temp = temp->next;
                }
            }//如果入度为0，则存入res
            if(flag) {res[idx++] = this->GraphList[i].data;visited[i] = 1;}
            flag = 1;//重置标记
        }
    }
}

DFS实现(栈+判环)

上面我们指出，拓扑排序可由 Kahn 算法得出，而 Kahn 算法实际上是一种 宽度优先搜索算法。那么，是否深度优先搜索算法也能用于求解拓扑排序问题呢？

答案是肯定的。
考虑图$G$ 通过 DFS 得到的深度优先生成森林。
森林中的每一颗树，其根结点就是这个树的所有结点中理应要最早完成的，并且其子孙结点必然在它完成之后才能开始进行。也就是说，对于生成森林中任一一棵树来说，结点所在的层次越小，该结点相对于这棵树就应该越早完成，该结点在拓扑序列中越靠前。
若按照编号依次进行 DFS，则生成森林中的后一颗树中的某个结点在$G$ 里可能指向前一棵树的根结点，也可能完全与前一棵树的根结点没关系。
也就是说，后一颗树要么是 独立的，这说明这棵树构成的拓扑序列和前一棵树互不干扰；要么它先于前一棵树的根结点完成。所以，为了保证拓扑排序正确，我们可以规定后一颗树的所有结点在拓扑排序中的位置始终处于前一棵树的所有结点之前。(拓扑排序可能不具有唯一性)

以下图为例，我们规定从编号 0 开始 DFS。

其 深度优先生成森林如下图所示：

从右到左，从上往下将结点纳入结果表，就能得到最终的拓扑序列：
$8→7→2→3→0→6→9→11→12→10→5→4→1$

可以发现，这种从后往前保存的操作，我们可以通过栈来实现！！

此外，为了判定图是否有环，我们还可以对原来 DFS 使用的 visited[] 数组的内容进行拓展。规定：
visited[i] = 0：未访问结点$V_i$；
visited[i] = 1：结点$V_i$ 已经被访问，且$V_i$ 及其子结点不含环；
visited[i] = -1 ：结点$V_i$ 已经被访问，且是父结点。

最终，我们可以得出代码如下：

int visited[MAX_VERTEX_NUM]; //访问标记数组
stack<int> List; // 存储最终拓扑结果

bool DFS_Topological(Graph G){
	/*
		DFS实现图G的拓扑排序，有环则返回 false
	*/
	memset(visited,0,sizeof(vis)); //标记数组初始化
	for(int i = 0; i < G.vexnum; i++){
		if(!visited[i] && !dfs(G,i))
			return false;
			 //处理每一个顶点，即得出完整的生成森林
			 //若有环则返回 false
	}
	return true;
}

bool dfs(G, v){
	/*
		dfs递归实现图遍历，有环则返回 false
	*/
	if(!visited[v]){
		visited[v] = -1; //打上根结点访问标记
	}
	//访问邻接点
	for(w = FristNeighbor(G,v); w >= 0; w = NextNeighbor(G,v,w)){
		if(visited[w] < 0)
			return false; //与根结点形成回路，即有环
		if(!visited[w] && !dfs(G,w)){
			return false; //子孙结点有环
		}
	}
	visited[v] = 1; 
	//子孙结点遍历结束后，把 v 还原为普通访问标记
	//以免生成森林中其他树在遍历时被误判为有环
	
	List.push(v);//结点压入栈中
	
	return true;
}

🔔整个算法，如果把最后的堆栈步骤删掉，就是纯粹的判定有向图是否有环的代码了。
🔔如果不用栈存储，而是队列，则输出的是逆拓扑有序

拓扑排序与邻接矩阵

若利用邻接矩阵存储有向图，某有向图的邻接矩阵中主对角线以下的元素均为零。则关于该图的拓扑序列 存在，可能不唯一。

证明如下：
根据题意，有邻接矩阵$A=(a_{ij})$，其中当$i\geq j$ 时，$a_{ij}=0$ （取等是因为默认无自环，即没有自身到自身的情况）。即：

$$A=\begin{bmatrix}0 & a_{12}& a_{13}&\cdots&a_{1n}\\& 0&a_{23}&\cdots&a_{2n}\\& & \ddots \\& & & 0&a_{n-1,n}\\&&&&0 \end{bmatrix}:=\begin{bmatrix}0&\alpha\\\mathbf0&A'\end{bmatrix}$$

显然，当$a_{12}\neq0$ 时，拓扑排序中结点$V_1$ 排在首位，然后删除与$V_1$ 相关的边，此时问题转化为一幅新的图的拓扑排序问题。而新图的邻接矩阵就是$A'$. 所以，若$\forall i,\;a_{i,i+1}\neq0$，则将依次输出$V_1,V_2,\cdots,V_n$，此时拓扑序列唯一。

而当$a_{12}=0$ 时，观察$A$ 可发现，此时$V_1,V_2$ 均是入度为0的结点，二者的顺序可交换，所以此时拓扑序列不唯一。

关键路径|_{Critical Path}

在上一节我们说过的拓扑排序主要是为解决一个工程能否顺序进行的问题，但有时我们还需要解决工程完成需要的最短时间问题。如果要获得一个工程流程拓扑图的最短时间，就必须要分析它们的拓扑关系，并且找到当中最关键的流程，关键流程所需的时间就是整个工作所需的最短时间。

AOE网

在一个表示工程的带权有向图中，用顶点表示事件，用有向边表示活动，用边上的权值表示活动的持续时间，这种用有向图的边表示活动的网，称为AOE网（Activity On edge Network)。

一个工程有且仅有一个开始、一个结束。对应地，AOE网只有一个源点一个汇点。

• 源点(起点)：AOE网中入度为0的顶点，表示整个工程的开始。
• 汇点(终点)：AOE网中出度为0的顶点，表示整个工程的结束。

既然AOE网是表示工程流程的，所以就具有明显的工程属性。只有在某顶点代表的事件发生后，从该顶点出发的各活动才能开始。只有在进入某顶点的各活动都已经结束，该顶点代表的事件才能发生。

应当掌握 AOE 和 AOV 网的区别。
AOV网是顶点表示活动的网，它只描述活动之间的制约关系；
而AOE网是用边表示活动的网，边上的权值表示活动持续的时间。

应该注意，从源点到汇点具有最大长度的路径叫关键路径，在关键路径上完成的活动叫关键活动。显然就 图7-9-3 的AOE网而言，【开始→发动机完成→部件集中到位→组装完成】就是关键路径，路径长度为$3+0.5+2=5.5$。

🔔【工作的最短时间】应当和所谓的【最短时间】作区分。
诚然，当我们真的只关注源点到汇点的最短时间的话，上图中最短的肯定是【开始→轮子完成→部件集中到位→组装完成】这条路径，路径长度：$0.5+0.5+2=3$。但是这并不是本节我们所指的关键路径。
同样以上图为例，只有等【发动机完成】之后，事件【部件集中到位】才真正抵达。而这个事件之前的一系列事件可以并行也可以一个个去完成。显然，并行的时候花费的时间最短，但再短也得等【发动机完成】这个事件结束才到下一个事件。所以，此处我们说的工作最短时间是在这个意义上的。

相关参量

通过以上分析，我们有：如果某项活动的最早开始时间和最晚开始时间一样，表示中间没有空隙，则此项活动就为关键活动

为此，我们需要明确每一个活动的时间情况，于是给定以下参量，供后续计算。

事件的最早/迟发生时间

事件$V_k$ 的最早发生时间$ve(k)$ |earliest time of vertex
—— 它是从源点$V_1$ 到某个顶点$V_k$ 的最长路径长度（可以理解为以$V_k$ 作为汇点的关键路径子问题）。它决定了$V_k$ 之后的活动能够开工的最早时间。

递推公式为：

$$ve(k)=\max_{\forall j\;,V_j\to V_k}\{ve(j)+w(V_j,V_k)\}$$

式中，$V_j$ 是$V_k$ 的任意前驱，$w(V_j,V_k)$ 则是有向边$V_j\to V_k$ 的边权（即工作时间）。

规定：$ve(1) = 0$. 即源点$V_1$ 的最早发生时间默认为0。

计算时，我们通常是从源点往后计算，所以采用从前往后的更新方法计算每个点的$ve()$ 值。
即列出$V_j$ 的所有后继，对后继作更新：

$$ve(k)\leftarrow\max\{ve(k),\;ve(j)+w(V_j,V_k)\}$$

其中，$V_k$ 是$V_j$ 的任一后继。

---

事件$V_k$ 的最迟发生时间$vl(k)$ |latest time of vertex
—— 它是指在不推迟整个工期的前提下，该事件最迟发生时间。也就是顶点$V_k$ 对应的事件最晚需要开始的时间，超出此时间将会延误整个工期。

递推公式为：

$$vl(k)=\min_{\forall j\;,V_k\to V_j}\{vl(j)-w(V_k,V_j)\}$$

式中，$V_j$ 是$V_k$ 的任意后驱，$w(V_j,V_k)$ 是有向边$V_k\to V_j$ 的边权.

规定：$vl(n) = ve(n)$，$V_n$ 是汇点。

计算时，我们通常是从汇点往前计算，所以采用从后往前的更新方法计算每个点的$vl()$ 值。
即列出$V_j$ 的所有前驱，对前驱作更新：

$$vl(k)\leftarrow\min\{vl(k),\;vl(j)-w(V_k,V_j)\}$$

其中，$V_k$ 是$V_j$ 的任一前驱。

活动的最早/迟开始时间

某个活动$A_i$ 对应着一段有向边，设为$<V_k,V_j>$。则：

$A_i$ 的最早开始时间$e(i)$ |earliest time of edge —— 它是该活动的起点表示的事件的最早发生时间，即：$e(i)=ve(k)$.

$A_i$ 的最迟开始时间$l(i)$|latest time of edge —— 它是该活动的终点表示的事件的最迟发生事件与该活动所需时间之差，即$l(i)=vl(j)-w(V_k,V_j)$.

一个活动的最迟开始时间与其最早开始时间的差额记为$d(i)=l(i)-e(i)$ —— 它是该活动完成的时间余量，即在推迟工期完成时间的情况下，活动$A_i$ 可以拖延的时间。

如果一个活动的$d()=0$ 说明它必须如期完成，一刻不能耽误，所以$d()=0$ 的活动均为关键活动。

关键路径

求关键路径的算法步骤如下：

1. 从源点$V_1$ 出发，令$ve(1) = 0$，按拓扑有序求出所有顶点(事件)的最早发生时间$ve()$
2. 从汇点$V_n$ 出发，令$vl(n) = ve(n)$，按拓扑逆序求出所有顶点(事件)的最迟发生时间$vl()$
3. 根据各顶点的$ve()$ 值求出所有边(活动)的最早开始时间$e()$
4. 根据各顶点的$vl()$ 值求出所有边(活动)的最迟开始时间$l()$
5. 求各顶点的差额$d()=e()-l()$ ，则$d()=0$ 的边构成关键路径，关键路径上的顶点为关键活动

下面给出一实例。

$$\begin{aligned}&Step0:ve(1)=0,拓扑排序序列：V_1,V_2,V_3,V_4,V_5,V_6\\\\&Step1:更新V_1的后继\;ve()\;值:\begin{cases}ve(2)=ve(1)+a_1=3\\ve(3)=ve(1)+a_2=2\end{cases}\\&Step2:更新V_2的后继\;ve()\;值:\begin{cases}ve(4)=ve(2)+a_3=5\\ve(5)=ve(2)+a_4=6\end{cases}\\&Step3:更新V_3的后继\;ve()\;值:\begin{cases}ve(4)=\max(ve(3)+a_5,ve(4))=6\\ve(6)=ve(3)+a_6=5\end{cases}\\&Step4:更新V_4的后继\;ve()\;值:ve(6)=\max(ve(4)+a_7,ve(6))=8\\&Step5:更新V_5的后继\;ve()\;值:ve(6)=\max(ve(5)+a_8,ve(6))=8\end{aligned}$$

$$\begin{aligned}&Step0:vl(6)=ve(6)=8,拓扑逆序序列：V_6,V_5,V_4,V_3,V_2,V_1\\\\&Step1:更新V_6的前驱\;vl()\;值:\begin{cases}vl(4)=vl(6)-a_7=6\\vl(5)=vl(6)-a_8=7\end{cases}\\&Step2:更新V_5的前驱\;vl()\;值:vl(2)=vl(5)-a_4=4\\&Step3:更新V_4的前驱\;vl()\;值:\begin{cases}vl(3)=\min(vl(4)-a_3,vl(2))=4\\vl(3)=vl(4)-a_5=2\end{cases}\\&Step4:更新V_3的前驱\;vl()\;值:vl(1)=vl(3)-a_3=0\\&Step5:更新V_2的前驱\;vl()\;值:vl(1)=\min(vl(2)-a_1,vl(1))=0\end{aligned}$$

最终得到关键路径：$V_1\to V_3\to V_4\to V_6$

---

🔔注意

关键路径上的活动是关键活动，它是决定整个工程工期的关键因素，即可以通过加快关键活动来缩短整个工程的工期。但是关键活动的缩短存在一个下限，因为一旦缩短到一定的程度，这条路径就不再是关键路径，该关键活动就会变成非关键活动。

AOE网的关键路径并不唯一，即关键路径可能有多条。且对于有几条关键路径的网，只加快一条关键路径上的关键活动并不能缩短整个工程的工期，只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的。

---

最小生成树|_{Minimum Spanning Tree,MST}

详见本站文章 👉🏻Huffman、Optimal-BST & MST| 算法之于树

在上述文章中，详细介绍了最小生成树的两种算法 Prim 和 Kruskal ，包括其算法思想、正确性证明、伪代码以及编程实现。
该文章总体思想来源于《算法导论》，其中给出的的复杂度分析也是基于最优情况，所以此处作一些额外的补充。

算法的复杂度

不采用优先队列，而直接利用暴力循环查找最小边时，Prim 算法的时间复杂度为$O(|V|^2)$，不依赖边集大小，它适用于边稠密图的最小生成树。

而 Kruskal 算法的时间复杂度一般认定为$O(|E|\log |E|)$，适用于边稀疏且顶点多的图的最小生成树。

但是，一般情况下都使用 Kruskal 算法，在稠密图尤其是完全图上，Prim 的复杂度虽然比 Kruskal 优，但 不一定 实际跑得更快。

相关性质

1. 无向连通图必定存在最小生成树，当相同权值的边有多条时，生成树结果可能不唯一，此外一定唯一，但是代价一定唯一；
2. 当最小生成树唯一时，Kruskal 和 Prim 算法均能得到相同的结果；
3. 最小生成树的$n-1$ 个边不一定是图中权值最小的$n-1$ 个边，因为最小的边不一定能使得图连通，也就谈不上构成一棵树了。

破圈法

---

最短路径|_{Shortest Path}

对于一个 有向带权连通图$G=(V,E,W)$ ，最短路径问题就是寻找给定源点$s\in V$ 到$G$ 中其他顶点$v\in V$ 的一条路径$p=<v_0,v_1,\cdots,v_k>$ 使得当$v_0=s,v_k=v$ 时$w(p)$ 的值最小。
其中，

$$w(p)=\sum_{i=0}^{k-1}w(v_i,v_{i+1})$$

为该路径上所有边权之和。$w(i,j)$ 是连接顶点$i,j$ 的边$e=<i,j>$ 的权重。

令$u$ 到$v$ 的最短路径权重为$\delta(u,v)$，则有，

$$\delta(u,v)=\begin{cases}\min\limits_{p\in P}w(p)&,P\text{ 为所有 }u\to v\text{ 的路径构成的集合},P\neq\varnothing\\ \infty&,\not\exists\text{ 路径 }p\text{ 使得 }u\to v\end{cases}$$

所以，$u$ 到$v$ 的最短路径就是使得$w(p)=\delta(u,v)$ 的路径$p$.

🔔注：在此处的定义重，边权有可能为负数！

最优子结构

可以证明最短路径问题具有最优子结构。
即：两个结点之间的最短路径中，包含有路径内其他结点之间的最短路径。

此处插入证明

最短路问题的分类

待更
主要讲单源、多源

Dijkstra 算法

Dijkstra（/ˈdikstrɑ/或/ˈdɛikstrɑ/）算法由荷兰计算机科学家 E. W. Dijkstra 于 1956 年发现，1959 年公开发表。是一种求解 非负权图 上单源最短路径的算法。

算法过程与伪代码

将结点分成两个集合：一组是已确定最短路径长度的点集（记为$S$ 集合），即源点$s$ 到任意结点$v\in S$ 都已求得最短路径。另一组集合是尚未确定最短路径长度的点集（记为$V-S$ 集合）。一开始所有的点都属于$T$ 集合。

初始化源点到自身的距离$dist(s,s)=0$，到其他点的距离$dist(s,v)$ 均为$+\infty$。

然后重复进行下列操作：

1. 从$V-S$ 集合中，选取一个源点到它的路径长度最小的结点$u$，加入到$S$ 集合中。
2. 对$u$ 的所有出边执行松弛操作，即讨论$u$ 的出边是否与$S$ 内的结点进行连接，然后相应地执行更新操作：若加入$u$ 之后使得$S$ 内其他结点的路径长度比原来更小，则这些结点更新为新路径。

直到$V-S$ 集合为空，算法结束。

$$\boxed{\large\begin{aligned} &\large\mathrm{Algorithm:Dijkstra}\\ &\\ &{\mathbf{Input:}}\mathrm{Directed\,\, graph\,\,}G=(V,E,W)\,\,\mathrm{with\,\, weight}\\ &\\ &{\mathbf{Output:}}\mathrm{All\,\, the\,\,shortest\,\,paths}\\ &\quad\quad\mathrm{\,\, from\,\, the\,\, source\,\,vertex\,\,}s\mathrm{\,\,to\,\,every\,\,vertex\,\,}v_i\in V\setminus\left\{s\right\}\\ &\\ &1:S\leftarrow \left \{ s \right \}\\ &2:\mathrm{dist}[s,s]\leftarrow 0\\ &3:{\mathbf{for}}\,\, v_i\in V-\left \{ s \right \}\,\,{\mathbf{do}}\\ &4:\quad\,\, \mathrm{dist}[s,v_i]\leftarrow w(s,v_i)\\ &\quad \,\,\,\quad (\mathrm{when\,\,}v_i\,\,\mathrm{not\,\,found},\mathrm{dist}[s,v_i]\leftarrow \infty)\\ &5:{\mathbf{while}}\,\,V-S\ne\varnothing \,\,{\mathbf{do}}\\ &6:\quad\,\,\,\, \mathrm{find\,\,}\min_{v_j\in V}\,\mathrm{dist}[s,v_j]\,\,\mathrm{from\,\, the\,\, set\,\,}V-S\\ &7:\quad\,\,\,\, S\leftarrow S\cup \left\{v_j\right\}\\ &8:\,\,\,\,\quad {\mathbf{for\,\,}}v_i\in V-S\,\,{\mathbf{do}}\\ &9:\,\,\,\,\,\,\,\quad\quad {\mathbf{if\,\,}}\mathrm{dist}[s,v_j]+w_{j,i}\lt\mathrm{dist}[s,v_i]\,\,{\mathbf{then}}\\ &10:\,\,\,\,\,\quad\quad\quad \mathrm{dist}[s,v_i]\leftarrow \mathrm{dist}[s,v_j]+w_{j,i} \end{aligned}}$$

实例演示

待更

时间复杂度

有多种方法来选取一个源点到它的路径长度最小的结点$u$，不同的实现导致了 Dijkstra 算法时间复杂度上的差异。

• 暴力：不使用任何数据结构进行维护，每次第二个操作执行完毕后，直接在$V-S$ 集合中暴力寻找最短路长度最小的结点。这使得第二步的时间复杂度为$O(|E|)$，而第一步的总时间复杂度为$O(|V|^2)$，全过程的时间复杂度为$O(|V|^2 + E) = O(|V|^2)$。
• 二叉堆：每成功松弛一条边$(u,v)$，就将$v$ 插入二叉堆中（如果$v$ 已经在二叉堆中，直接修改相应元素的权值即可），第一步操作直接取堆顶结点即可。共计$O(|E|)$ 次二叉堆上的插入（修改）操作，$O(|V|)$ 次删除堆顶操作，而插入（修改）和删除的时间复杂度均为$O(\log |V|)$，时间复杂度为$O((|V|+|E|) \log |V|) = O(|E| \log |V|)$。
• 优先队列：和二叉堆类似，但使用优先队列时，如果同一个点的最短路被更新多次，因为先前更新时插入的元素不能被删除，也不能被修改，只能留在优先队列中，故优先队列内的元素个数是$O(|E|)$ 的，时间复杂度为$O(|E| \log |E|)$。
• Fibonacci 堆：和前面二者类似，但 Fibonacci 堆插入的时间复杂度为$O(1)$，故时间复杂度为$O(|V| \log |V| + |E|) = O(|V| \log |V|)$，时间复杂度最优。但因为 Fibonacci 堆较二叉堆不易实现，效率优势也不够大，算法竞赛中较少使用。
• 线段树：和二叉堆原理类似，不过将每次成功松弛后插入二叉堆的操作改为在线段树上执行单点修改，而第一步则是线段树上的全局查询最小值。时间复杂度为$O(|E| \log |V|)$。

在稀疏图中，$|E| = O(|V|)$，使用二叉堆实现的 Dijkstra 算法较 Bellman-Ford 算法具有较大的效率优势；
而在稠密图中，$|E| = O(|V|^2)$，这时候使用暴力做法较二叉堆实现更优。

正确性证明

从算法过程中不难发现，dijkstra 算法属于贪心策略算法。因此，需要对其正确性进行证明。

待更

Floyd-Warshall 算法

动态规划。

$$d^{(k)}_{ij}=\begin{cases}w_{ij},&k=0\\ \min\limits_{}(d_{ij}^{(k-1)},d_{ik}^{(k-1)}+d_{kj}^{(k-1)}),&k\geq1 \end{cases}$$

滚动数组、状态压缩

for (k = 1; k <= n; k++) { 
	for (x = 1; x <= n; x++) { 
		for (y = 1; y <= n; y++) { 
			f[k][x][y] = min(f[k - 1][x][y], f[k - 1][x][k] + f[k - 1][k][y]); 
		}
	} 
}

传递闭包

https://oi-wiki.org/graph/shortest-path/#floyd-算法

事实上，Floyd 算法 适用于任何图，不管有向无向，边权正负，但是最短路必须存在。（不能有个负环）

二叉树转邻接表

对于二叉树的邻接表转换，需要明确：二叉树结点最多只有两个孩子结点，因此我们可以分为四种情况，通过递归的方式进行转换，算法思想如下：

1. 判断当前树是否为空，为空则返回当前下标不做处理，否则存入当前根结点；
2. 如果当前树有左右两个结点，则建立边链表，自增下标后存左子树，将左子树存毕后，将返回得到的新下标自增再存右子树，最终返回当前下标；
3. 如果当前树只有左结点，则建立边链表，自增下标后存左子树，最终返回当前下标；
4. 如果当前树只有右结点，则建立边链表，自增下标后存右子树，最终返回当前下标；
5. 如果当前树是叶子结点，则指链表为空，返回当前下标。

template<class elementType> 
int InsertBinTree(ALGraph<elementType> &graph,BinTree<elementType> *tree, int idx){
    //将二叉树转为邻接表存储
    //返回当前结点个数(当前插入邻接表之后的最大下标)
    int new_idx;
    if(tree->isNULL) return idx;
    graph.GraphList[idx].data = tree->root_data;
    if((!tree->left->isNULL) && (!tree->right->isNULL)){
        graph.GraphList[idx].first = new ArcNode();
        graph.GraphList[idx].first->VexIndex = idx+1;
        graph.GraphList[idx].first->weight = 1.0;
        new_idx = InsertBinTree(graph,tree->left,idx+1);
        graph.GraphList[idx].first->next = new ArcNode();
        graph.GraphList[idx].first->next->VexIndex = new_idx+1;
        graph.GraphList[idx].first->next->weight = 1.0;
        graph.GraphList[idx].first->next->next = NULL;
        new_idx = InsertBinTree(graph,tree->right,new_idx+1);;
        return new_idx;
    }
    else if(!tree->right->isNULL){
        graph.GraphList[idx].first = new ArcNode();
        graph.GraphList[idx].first->VexIndex = idx+1;
        graph.GraphList[idx].first->weight = 1.0;
        graph.GraphList[idx].first->next = NULL;
        idx = InsertBinTree(graph,tree->right,idx+1);
        return idx;
    }
    else if(!tree->left->isNULL){
        graph.GraphList[idx].first = new ArcNode();
        graph.GraphList[idx].first->VexIndex = idx+1;
        graph.GraphList[idx].first->weight = 1.0;
        graph.GraphList[idx].first->next = NULL;
        idx = InsertBinTree(graph,tree->left,idx+1);
        return idx;
    }
    else{
        graph.GraphList[idx].first = NULL;
        return idx;
    }
}
//设置对应的重载析构函数
template<class elementType> 
ALGraph<elementType>::ALGraph(BinTree<elementType> *tree){
    VexNum = InsertBinTree<elementType>(*this,tree,0)+1;
}