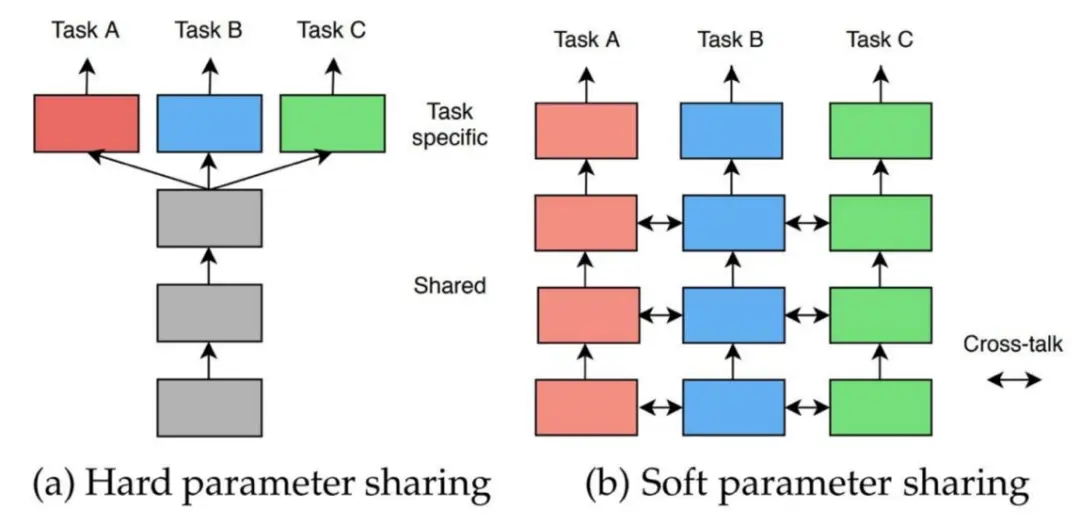
解空间与搜索树
介绍几个经典搜索问题及其数学模型
阐述从问题中抽象出来的解空间,利用搜索树的方式表示
通过树推广到图,然后引出图的遍历算法,此算法也是解空间的搜索算法
指出这些搜索算法本质上是盲目搜索,是暴力穷举的优化版
全排列问题
宽度优先搜索/BFS
宽度优先搜索(Breadth First Search),简称BFS,属于一种盲目搜寻法,目的是系统地展开并检查 图/解空间 中的所有 结点/解,以找寻结果。
BFS在求解最短路径的 Dijkstra 算法 和 最小生成树 的 Prim 算法中都有体现。
二叉树的层次遍历
所谓“二叉树的层次遍历”,简单来说就是从上到下,从左到右的顺序对二叉树的各个结点进行遍历。
例如,下图中的二叉树,其层次遍历的结果是 : 5 1 7 2 4 6 3

我们在数据结构的学习中指出,可以利用队列的特性,依次将每一个子树入队,等到需要使用时,再出队进行操作。如下图所示,我们可以利用队列得到这样的操作步骤:

伪代码如下:
1
2
3
4
5
6
7
8
9
10
11
|
LevelOrder(int root)
queue<int> Q ;创建一个队列
Q.push(root) ;将根结点入队列
while(队列不为空){
获得队首元素
将队首元素出队
输出当前结点的值
如果该结点的左儿子不为空,将左儿子加入到队列中
如果该结点的右儿子不为空,将右儿子加入到队列中
}
|
图的广度优先遍历
图的遍历 比 树的层次遍历要复杂得多。因为图中任一顶点都有可能和其余顶点相连。
按照上例中,树层次遍历的伪代码的说法就是:”将孩子加入到队列“中的时候,有可能把已经访问过的结点再次入队,导致同一顶点多次访问,甚至无限访问下去。
因此,为了让程序记下哪些结点是否访问过,我们需要增设一个新的数组 visited[] 用于标记某个顶点的访问情况。
于是,对于一幅连通图G(V,E) ,我们就可以按照层次遍历那样对其进行遍历了。
- 首先将初始顶点v0∈V 加入队列Q;
- 顶点出队,访问此出队的顶点vi ,为其打上标记 :visited[i]←1;
- 然后依次把该出队顶点的邻接点uj∈N(vi) 入队,回到第 2 步,直到队列为空。
而对于非连通图,只需对每个顶点都执行一次上述 BFS 操作,因为标记数组的加入可以使得属于某个连通分量的顶点也可以在遍历初期就跳出去,所以最终可以得到所有连通分量的遍历,综合起来就是整幅图的遍历结果了。
C++ 的 STL 为我们提供了 <queue> 类可以方便我们直接使用队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| int visited[MAX_VERTEX_NUM];
void BFSTraverse(Graph G){
memset(visited,0,sizeof(vis));
queue<Node> qu;
for(int i = 0; i < G.vexnum; i++){
if(!visited[i])
bfs(G,i);
}
}
void bfs(G, v){
qu.push(v);
while(!qu.empty()){
v = qu.front(); qu.pop();
if(!visited[v]){
cout << G.vex[v].data << " ";
visited[v] = 1;
}
for(w = FristNeighbor(G,v); w >= 0; w = NextNeighbor(G,v,w)){
if(!visited[w]){
qu.push(w);
}
}
}
}
|
奇怪的电梯 #HDU1548
先描述问题
抽象成数学语言
给出伪代码和AC代码
BFS 的万能模板
通过以上例题,我们可以不断总结出 BFS 在解决 ACM/OI 问题时的注意事项。
- 【树的层次遍历】让我们了解队列在宽度优先搜索中的核心地位与用法;
- 【图的 BFS 】让我们知道在实际求解问题时,应当设置标记数组避免循环访问;
- 【奇怪的电梯问题】让我们知道如何把问题改写成一个图搜索问题,从而进行求解。
最终,可以总结得出能套用的万能模板(伪代码):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| #include<queue>
using namespace std;
int vis[n维数组];
struct status{成员};
int bfs(所需变量){
status cur,nex;
int tmp;
queue<status> qu;
qu.push(cur);
memset(vis,0,sizeof(vis));
while(!qu.empty()){
cur = qu.front();
qu.pop();
if(符合要求) return 结果;
if(满足某某条件){
nex.成员 = 处理;
qu.push(nex);
}
if(满足某某条件){
nex.成员 = 处理;
qu.push(nex);
}
}
return 得不到的结果表示;
}
|
双端队列 BFS
优先队列 BFS
深度优先搜索/DFS
深度优先搜索(Depth First Search),简称DFS,与 BFS 一样,它也属于一种盲目搜寻法。
对比来看,BFS 是如其名一样,是尽可能先往宽度方向搜索解空间,然后再往下一层搜索,类似于树的层次遍历。而 DFS 也如其名,其过程简要来说是对每一个可能的分支路径深入到不能再深入为止地进行搜索,当然每个解点/解空间 也只能访问一次,类似于树的先序遍历。
它们目的都是系统地展开并检查 图/解空间 中的所有 结点/解,以找寻结果。
图的深度优先遍历
根据深度优先搜索的定义,我们可以推敲出其在图的遍历中的实际过程。
首先访问图的起始顶点v,然后从v 出发,访问与之邻接的第一个结点w ,再访问与w 邻接的第一个结点u ,如此下去,直到最深处访问完毕,但仍有结点未访问时,再往上一个点回溯,然后访问其下一个邻接点(如果有)。
不难发现,即使是 DFS,我们也需要记录某结点是否访问过,所以 visited[] 数组必不可少。
我们可以采用递归的方法给出其遍历算法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| int visited[MAX_VERTEX_NUM];
void DFSTraverse(Graph G){
memset(visited,0,sizeof(vis));
for(int i = 0; i < G.vexnum; i++){
if(!visited[i])
dfs(G,i);
}
}
void dfs(G, v){
if(!visited[v]){
cout << G.vex[v].data << " ";
visited[v] = 1;
}
for(w = FristNeighbor(G,v); w >= 0; w = NextNeighbor(G,v,w)){
if(!visited[w]){
dfs(G,w);
}
}
}
|
全排列问题的求解
DFS 的万能模板
通过以上例题,我们可以不断总结出 DFS 在解决 ACM/OI 问题时的注意事项。
- 【图的 DFS 】让我们知道在实际求解问题时,应当设置标记数组避免循环访问;
- 【全排列问题】让我们知道如何把问题改写成一个图搜索问题,从而进行求解;
还可以发现,事实上 dfs 就是一个递归求解+剪枝的过程。
最终,可以总结得出能套用的万能模板(伪代码):
记忆化搜索
在以前的文章中,我们探讨了斐波那契数列的一些计算方法,不仅如此还给出了其递推公式和通项公式。
详见👉🏻 快速幂算法与斐波那契数列
这里我们回顾一下,采用递归的形式展现斐波那契数列的计算:
1
2
3
4
5
6
7
8
|
int fibo(int a)
{
if(a==0 || a==1)
return 1;
else
return fibo(a-1) + fibo(a-2);
}
|
不难发现,当我们调用函数 fibo(3) 时,它一定会递归地调用 fibo(2), fibo(1)。而 fibo(2) 又会递归地调用 fibo(1), fibo(0)。其中,fibo(1) 重复调用了两次,但是函数还是基于内部逻辑对其重新计算了一遍。这显然是一种浪费。所以,如果用这种方法计算第n 项斐波那契的时候,会有大量的重复计算。
更直观地,如果画出该递归算法/该问题的搜索树,会有许多节点明明可以共用但是却重复出现。因此,把“计算过”的内容“记忆”下来,后面要用的时候直接拿来用 的思想就是所谓的记忆化搜索。
上面的代码我们就可以利用数组“记忆”计算结果。这在保证基本的递归结构不变的同时,利用空间换时间的方法,加快了搜索速度:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
#define maxn 100000
long long f[maxn];
int fibo(int a)
{
if(f[a] != -1) return f[a];
if(a==0 || a==1)
{
f[a] = 1;
}
else
{
f[a] = fibo(a-1)+fibo(a-2);
}
return f[a];
}
int main(void)
{
int n;
memset(f, -1, sizeof(f));
cin >> n;
cout << fibo(n);
}
|
分支定界法
经典例题
装载问题| Optimal Loading Problem
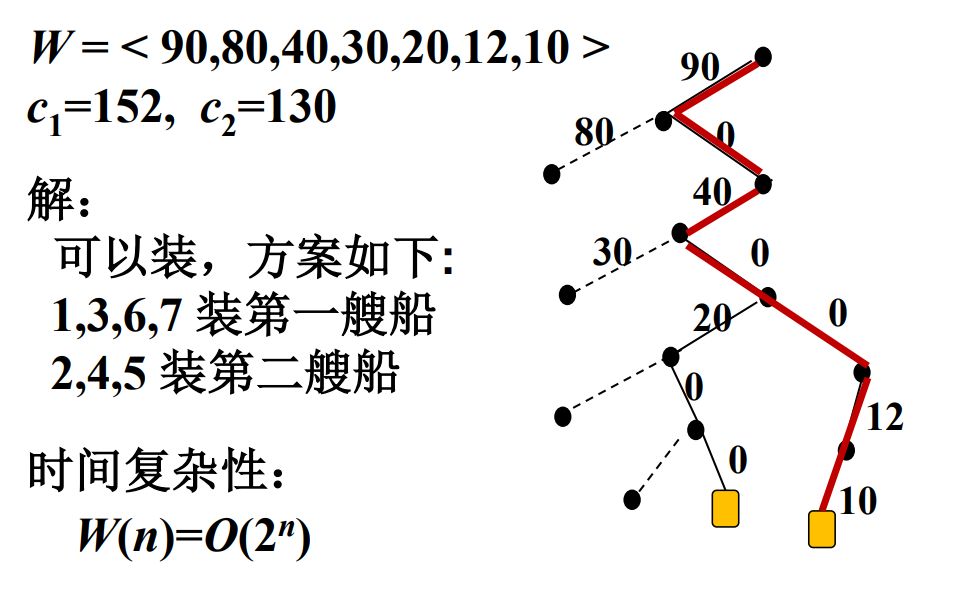
有n 个集装箱,需要装上两艘载重分别为c1 和c2 的轮船。wi 为第i 个集装箱的重量,显然要求有:
i=1∑nwi≤c1+c2
问: 是否存在一种合理的装载方案把这n 个 集装箱 装上船. 如果有,请给出一种方案。
很容易想到一种策略,我们先将尽量多的集装箱可能地装入其中一艘轮船上,不妨设为载重为c1 的那一艘。从而构建一种求解该问题的 0-1 解空间X=<x1,x2,...,xn> 最优化下面的目标函数:
minc1−i=1∑nwixi
其中,xi={1,0,将第 i 个集装箱装入else
那么当下式成立时,可以判断存在装载方案使得问题解决。
i=1∑nwi(1−xi)≤c2
为了求解该问题,我们可以先对W 进行排序,使得集装箱的重量W=(w1,w2,...,wn) 满足w1≤w2≤⋯≤wn。
然后依次放入第一艘轮船,放不下就继续访问下一个直到所以的集装箱均访问完毕。这样得到一趟可行解之后,我们再从后往前回溯,找到从后往前看的加入轮船的第一个集装箱i,此时的解空间中x[i]=1。将其置 0 并讨论不将其加入的情况,继续装箱即可得到另一种决策情况。
这样不断回溯,直到回溯到第一个集装箱,即i=1 时,所有的可行解已经搜索完毕。我们用一个变量best 保存回溯过程中的当前最优值,最终即可得到最优解。
根据上面的描述。我们可以采用迭代而非递归的方法给出算法伪码:
1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.Algorithm: Loading(W,c1,n)Sort(W)B←best←c1i←1;sum←0repeatwhilei≤ndoifsum+wi≤c1thensum←sum+wix[i]←1;B←B−wielsex[i]←0ifB<bestthenbest←Band记录解Xwhilei>1andx[i]=0do//回溯i←i−1ifx[i]=1thenx[i]←0;B←B+wi;sum←sum−wiuntili=1returnbest,X
每一个集装箱对应的解向量元素都有 0, 1 两种可能,依次该算法的时间复杂度为O(2n),考虑到需要记录解空间,所以空间复杂度为O(n)。
假设给定如下输入,图的右边是具体的解空间树,下面我们将利用 c++ 编程进行验证。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| #include <iostream>
#include <string.h>
#include <vector>
#include <cstdlib>
using namespace std;
#define M 100
int best_x[M];
void loading(int w[], int c, int n){
int B = c, best = c;
int i = 1, j = 1, sum = 0;
int *x = (int *)malloc(sizeof(int)*n);
memset(x,0,sizeof(x));
memset(best_x,0,sizeof(best_x));
do{
while(i <= n){
if(sum + w[i-1] <= c){
sum += w[i-1]; B -= w[i-1];
x[i-1] = 1;
}else x[i-1] = 0;
i++;
}
if(B < best){
best = B;
for(int k = 0; k < n; k++){
best_x[k] = x[k];
}
}
i--;
while(i > 1 && x[i-1] == 0) i--;
if(x[i-1] == 1){
B += w[i-1]; sum -= w[i-1];
x[i-1] = 0;
i++;
}
}while(i != 1);
}
int main(void){
int W[7] = {90, 80, 40, 30, 20, 12,10};
int c1 = 152, c2 = 130;
loading(W, c1, 7);
int sum = 0;
cout << "X = (";
for(int i = 0; i < 7; i++){
cout << best_x[i] << " ";
sum += W[i]*(1-best_x[i]);
}
cout << ") ";
if(sum <= c2) cout << "[YES]" << endl;
return 1;
}
|
图着色问题| Graph Coloring Problem, GCP
给定一个无向连通图G=(V,E) 和m 种不同的颜色,如果用这些颜色为图G 的各顶点着色,每个顶点只能着一种颜色,并且要求图中每条边连接的两个顶点着不同颜色。这样的问题被称为图着色问题(GCP)。
图着色问题还可以表述为将图G 的点集V 分为m 个颜色组,每组形成一个独立集,即组与组之间没有相邻的顶点。
图的m 着色优化问题就是指找到满足上述约束条件的最小颜色数m∗. 称m∗ 为图G 的最小色数。
事实上,著名的 四色定理 (世界近代三大数学难题之一)指出:
每个平面地图都可以只用四种颜色来染色,而且没有两个邻接的区域颜色相同。
之所以是难题,是因为目前并没有严密的逻辑证明,但是计算机对数以万计的平面图进行验证该定理均成立。
下面将对图的m 着色判定问题进行算法实现。
图的m 着色判定问题要求,对给定的图G 和色数m 判定能否在满足约束的情况下实现着色,如果能则给出着色方案,如果不能则输出 No.
显然我们可以通过回溯算法解决该问题。可以根据对称性,将颜色标记进行全排列后仍是一种着色方案。所以只需搜索1/m 的解空间。所以为了加快搜索效率,避免重复计算,我们可以提前对一个结点的着色方案进行确定。
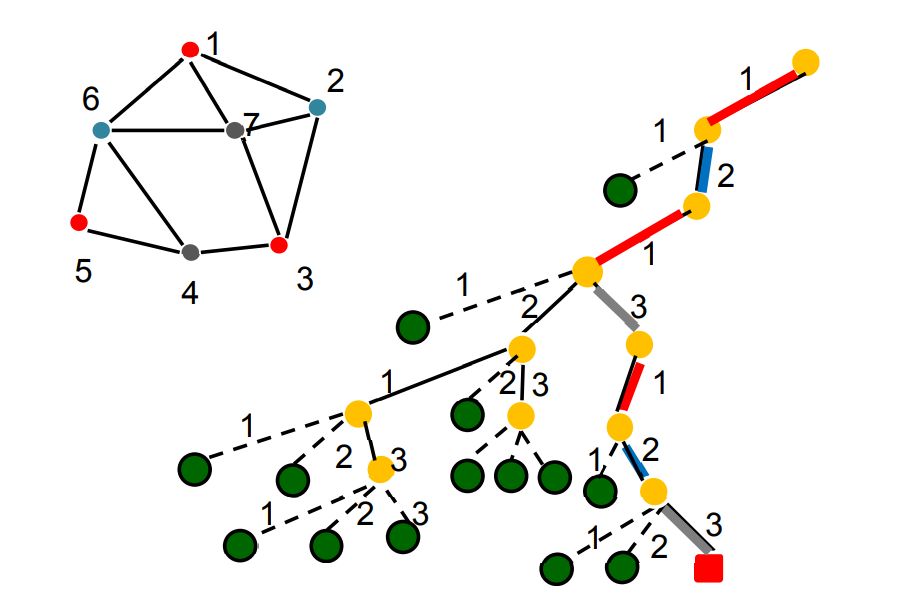
事实上,如果对 结点1 定下一种颜色,再对与 1 相连的另一个结点 (如 结点2 )也固定颜色后,就可以得到完全不重复的解。
- 用step 表示当前分支的第step 个结点标号。
- 用color[1..n] 存储当前分支的解(着色情况)。
- 用Adj[x] 表示与结点x 相连的结点集合
算法的伪码如下:
1.2.3.4.5.6.7.Algorithm: GCP-DFS(step)ifstep=n+1thenreturnTruefori=1tomdocolor[step]←iforeachnode∈Adj[step]doifcolor[node]=color[step]thenreturnGCP-DFS(step+1)color[step]←0//回溯
分析伪码得知,最坏情况下无向图为完全图,此时每一个结点下都要搜索与之相连的n−1 个结点,每一个结点的着色都有 1, 2, ..., m 种可能。所以此算法的时间复杂度为O(nmn).
由于回溯过程中需要记录当前状况下的着色情况,所以其空间复杂度与解空间大小一致,大小为O(n).
用下图所示的示例进行编程验证:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
| #include <iostream>
#include <string.h>
#include <vector>
#include <cstdlib>
using namespace std;
#define M 100
struct ADJ{
vector<int> nodes;
}Adj[7];
int n = 7, m = 3;
int visited[M] = {0};
int col[M] = {0};
bool check(int step, int color){
for(int i = 0; i < Adj[step-1].nodes.size(); i++){
if(col[Adj[step-1].nodes[i]] == color){
return false;
}
}
return true;
}
void dfs(int step){
int i;
if(step == n+1){
cout << "[Yes]" << endl;
for(int i = 1; i <= n; i++){
cout << "node " << i << ": " << col[i] << endl;
}
return;
}
for(i = 1; i <= m; i++){
if(check(step, i) == 1){
col[step] = i;
dfs(step+1);
col[step] = 0;
}
}
}
int main(void){
Adj[0].nodes = {2, 6, 7};
Adj[1].nodes = {1 ,3 ,7};
Adj[2].nodes = {2, 4 ,7};
Adj[3].nodes = {3, 5, 6};
Adj[4].nodes = {4, 6};
Adj[5].nodes = {1, 4, 5, 7};
Adj[6].nodes = {1, 2, 3, 6};
col[1] = 1; col[2] = 2; dfs(3);
cout << "END" << endl;
return 1;
}
|
圆排列问题
待更
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
| #include<bits/stdc++.h>
using namespace std;
const int maxn = 12;
int n;
int r[maxn], vis[maxn], ans[maxn];
double L[maxn], x[maxn];
double d, best;
int min_r(int cur) {
int res = INT_MAX;
for(int i = 1; i <= n; i++){
if(vis[i] == 0){
res = min(res, r[i]);
}
}
return min(res, ans[cur]);
}
void calculate(int cur) {
x[cur] = 0;
for(int i = 1; i < cur; i++){
d = 2*sqrt(ans[i]*ans[cur]);
x[cur] = max(x[cur], x[i]+d);
}
}
void update_solve(void) {
double left = 0, right = 0;
for(int i=1; i<=n; i++){
left = min(left, x[i]-ans[i]);
right = max(right, x[i]+ans[i]);
}
best = min(best, right-left);
}
void dfs(int cur) {
if(cur == n+1){
update_solve();
return;
}
for(int i = 1; i <= n; i++){
if(vis[i] == 0){
ans[cur] = r[i];
calculate(cur);
vis[i] = 1;
dfs(cur+1);
vis[i] = 0;
}
}
}
int main(void){
while(cin >> n){
best = 0x3f3f3f3f;
memset(vis, 0, sizeof(vis));
for(int i = 1; i <= n; i++){
cin >> r[i];
}
dfs(1);
printf("%.3lf\n", best);
}
return 0;
}
|
参考:https://blog.csdn.net/holly_Z_P_F/article/details/121922245
参考
- HDForum-DFS&BFS|by杭电刘春英
- DFS深度优先搜索|CSDN
- 图着色问题(回溯法)|CSDN