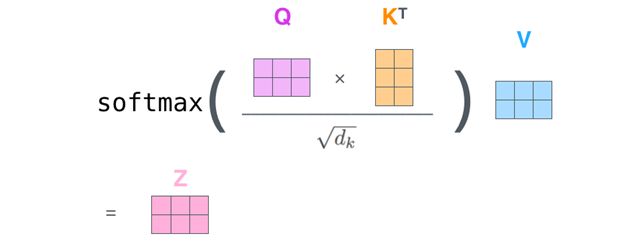Motivation | 起源

状态空间表示法

在现代控制理论中，状态是指在一个动态系统中可以用于决定系统状态的最小数目的变量的有序集合。而状态空间则是指该系统全部可能的状态的集合。

状态空间表示法即为一种将系统表示为一组输入、输出及状态的数学模式，而输入、输出及状态之间的关系用多个一阶微分方程来描述。一般地，考虑多输入多输出情况的时变系统时，我们用向量形式表达：

x˙=f(x,u,t)y=g(x,u,t)\begin{aligned} \dot{\boldsymbol x}&=\boldsymbol{f}(\boldsymbol x,\boldsymbol u,t)\\ \boldsymbol y&=\boldsymbol{g}(\boldsymbol x,\boldsymbol u,t) \end{aligned}

其中，x\boldsymbol x 为状态向量，u\boldsymbol u 为输入信号向量/控制向量，y\boldsymbol y 是输出向量，而x˙:=dxdt\dot{\boldsymbol x}:=\dfrac{\mathrm d\boldsymbol x}{\mathrm dt} 。

特别地，考虑线性系统时，我们有：

x˙(t)=A(t)x(t)+B(t)u(t)y(t)=C(t)x(t)+D(t)u(t)\begin{aligned} \dot{\boldsymbol x}(t)&=\boldsymbol{A}(t)\boldsymbol x(t)+\boldsymbol{B}(t)\boldsymbol u(t)\\ \boldsymbol y(t)&=\boldsymbol{C}(t)\boldsymbol x(t)+\boldsymbol{D}(t)\boldsymbol u(t) \end{aligned}

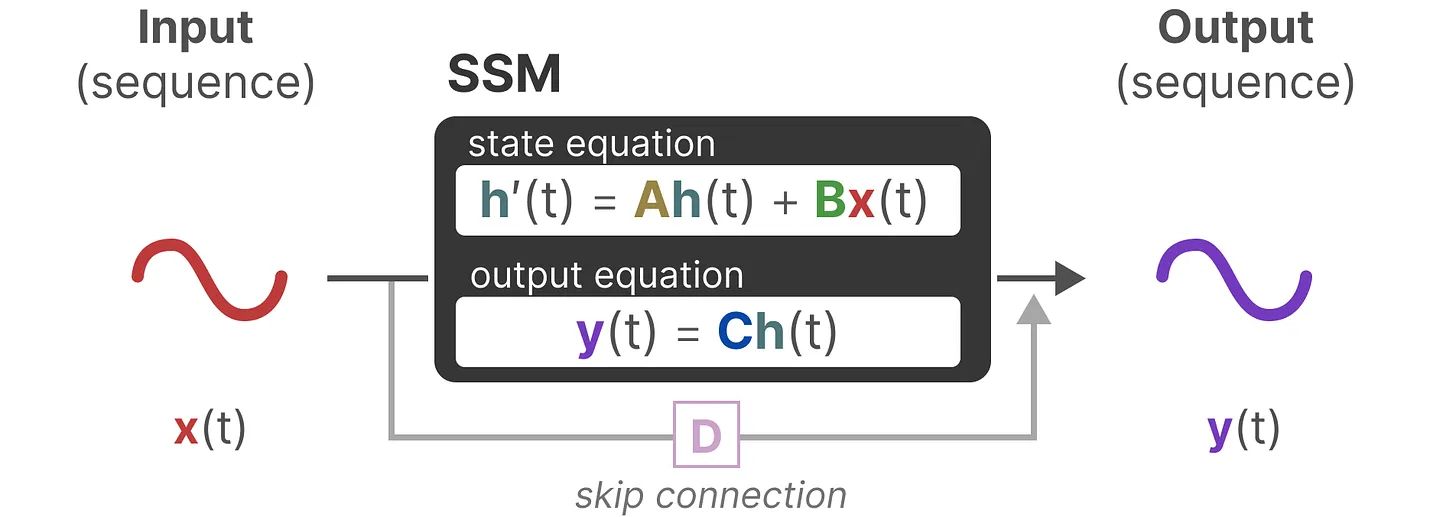
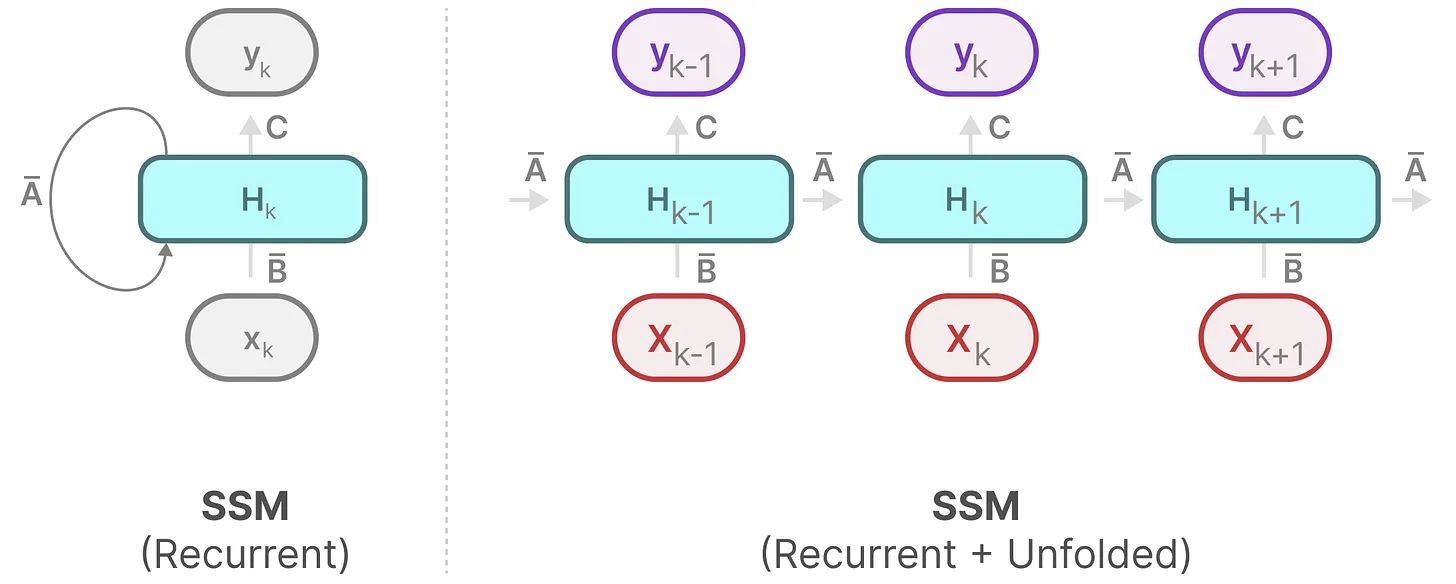
而状态空间模型（State Space Model，SSM）则是沿用了这种看待物理系统的视角，使用单输入单输出的线性时不变系统来建模一个有输入有输出的机器学习模型，固定四个系数矩阵不变。如果采用机器学习中比较常用的数学符号重新书写上述方程，即可得到：

h˙(t)=Ah(t)+Bx(t)y(t)=Ch(t)+Dx(t)\begin{aligned} \dot{\boldsymbol h}(t)&=\boldsymbol{A}\boldsymbol h(t)+\boldsymbol{B}x(t)\\ y(t)&=\boldsymbol{C}\boldsymbol h(t)+\boldsymbol{D}x(t) \end{aligned}

其中h(t)∈RN\boldsymbol h(t)\in\mathbb R^N 表示隐状态向量，x(t)∈Rx(t)\in\mathbb R 则是标量单输入（维数是 1），A,C∈RN×N,B,D∈RN\boldsymbol {A},\boldsymbol {C}\in\mathbb R^{N\times N}, \boldsymbol {B},\boldsymbol {D}\in\mathbb R^{N}，NN 是隐状态的维度。

更进一步地，沿用深度学习的思考方式， 输出步的Dx(t)\boldsymbol{D}x(t) 实际上是一种跳接策略，所以一个SSM模块我们还可以在输出方程部分精简成y(t)=Ch(t)y(t)=\boldsymbol{C}\boldsymbol h(t).

另外，为了将输入从一维扩展到多维的情况，SSM通过对每一个维度都独立执行单值输入SSM的方式得到多输入多输出的SSM，而不是传统线性控制理论中的多输入多输出系统那样。

微分方程的求解

事实上，该微分方程满足一阶线性非齐次微分方程的形式，因此可以直接套公式求解得到：

h(t)=eAt(B∫0tx(τ)e−Aτdτ+C)\boldsymbol h(t)=e^{\boldsymbol At}\biggl(\boldsymbol B\int_{0}^tx(\tau)e^{-\boldsymbol A\tau}\mathrm d\tau+C\biggr)

此处的非粗体CC 表示任意常数。

给定初值h(0)\boldsymbol h(0) 可得：

h(t)=h(0)eAt+BeAt∫0tx(τ)e−Aτdτ\boldsymbol h(t)=\boldsymbol h(0)e^{\boldsymbol At}+\boldsymbol Be^{\boldsymbol At}\int_{0}^tx(\tau)e^{-\boldsymbol A\tau}\mathrm d\tau

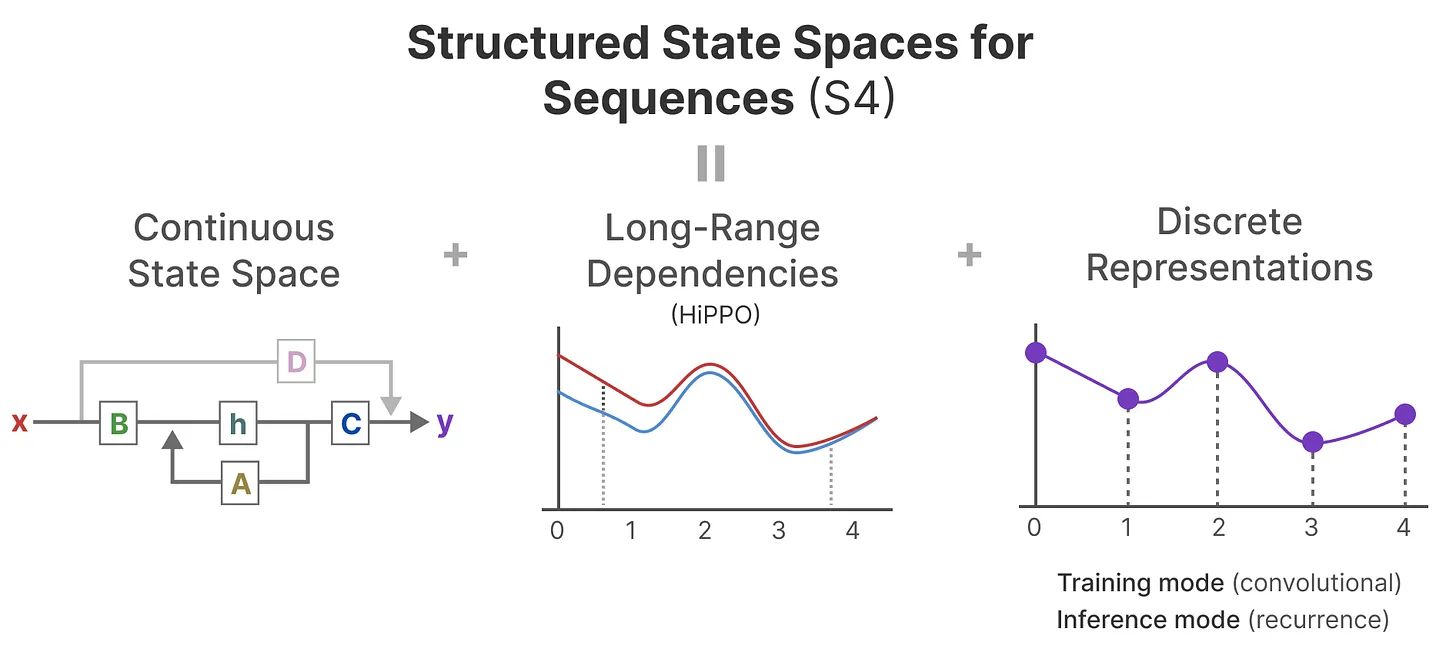
S4: 结构化SSM

Efficiently Modeling Long Sequences with Structured State Spaces (arxiv.org)

离散化处理

SSM的原始表达针对的是连续信号，而如果要将它视为机器学习模型，我们希望它同样可以作用于离散输入。实际上在工程中往往输入的也只是连续信号的采样。

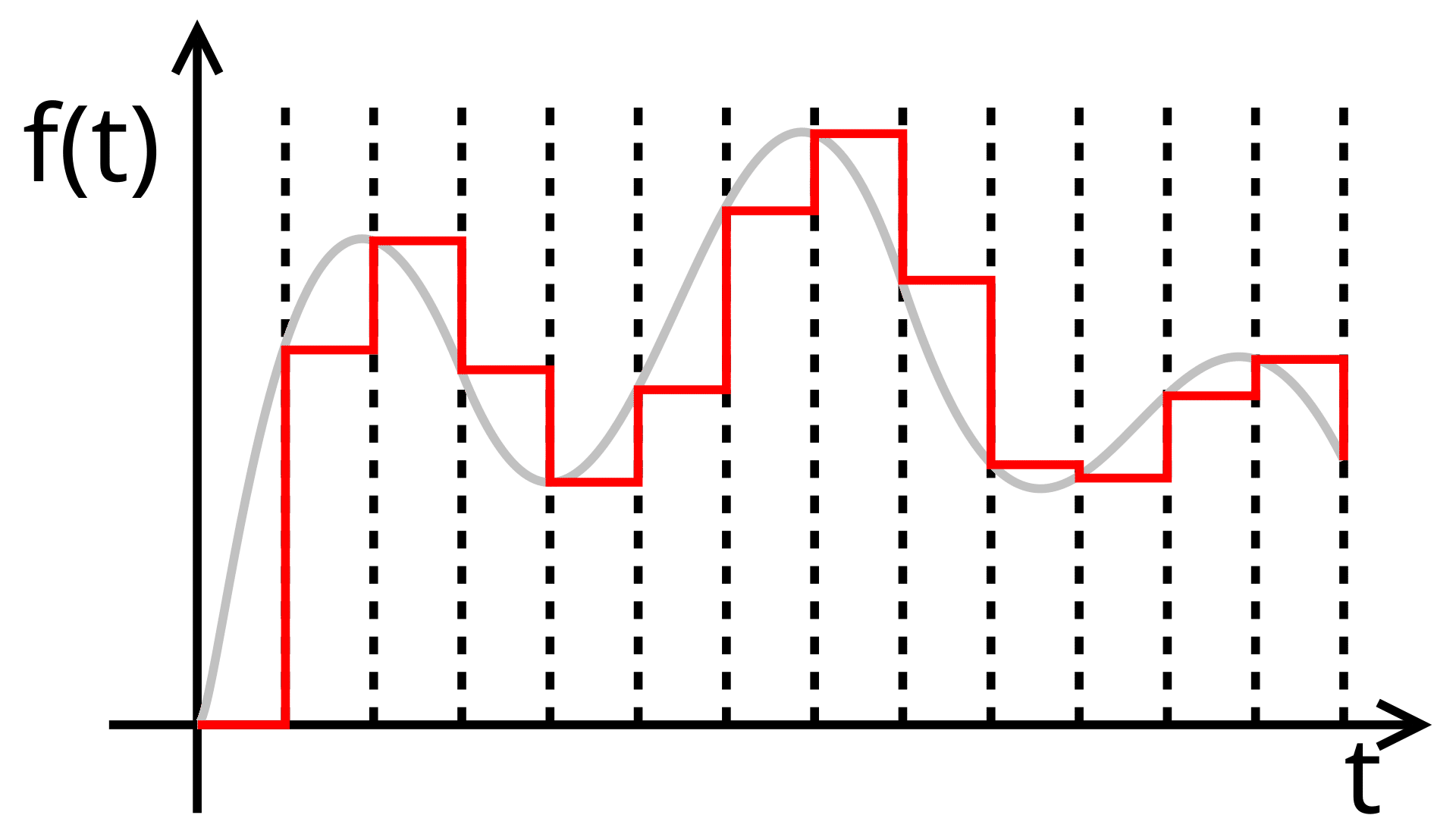
而处理离散值的一个最有效的方法就是利用 零阶保持技术(Zero-order hold technique) 将离散值转化为连续值。

如图所示，零阶保持将每一个时刻tt 的采样值保持原来的值不变，直到到达下一个采样时间t+Δt+\Delta ， 即x(t+Δ)=x(t)x(t+\Delta)=x(t)。

从而我们有：

h(t+Δ)=h(0)eA(t+Δ)+BeA(t+Δ)∫0t+Δx(τ)e−Aτdτ=eΔA×[h(0)eAt+BeAt∫0tx(τ)e−Aτdτ]+BeA(t+Δ)∫tt+Δx(τ)e−Aτdτ=eΔA×h(t)+BeA(t+Δ)∫tt+Δe−Aτdτ×x(t)=eΔA×h(t)+A−1(eΔA−I)B×x(t)=eΔA×h(t)+(ΔA)−1(eΔA−I)ΔB×x(t):=A‾h(t)+B‾x(t)\begin{aligned} \boldsymbol h(t+\Delta)&=\boldsymbol h(0)e^{\boldsymbol A(t+\Delta)}+\boldsymbol Be^{\boldsymbol A(t+\Delta)}\int_{0}^{t+\Delta}x(\tau)e^{-\boldsymbol A\tau}\mathrm d\tau\\ &=e^{\Delta \boldsymbol A}\times\left[\boldsymbol h(0)e^{\boldsymbol At}+\boldsymbol Be^{\boldsymbol At}\int_{0}^{t}x(\tau)e^{-\boldsymbol A\tau}\mathrm d\tau\right]+\boldsymbol Be^{\boldsymbol A(t+\Delta)}\int_{t}^{t+\Delta}x(\tau)e^{-\boldsymbol A\tau}\mathrm d\tau\\ &=e^{\Delta \boldsymbol A}\times\boldsymbol h(t)+\boldsymbol Be^{\boldsymbol A(t+\Delta)}\int_{t}^{t+\Delta}e^{-\boldsymbol A\tau}\mathrm d\tau\times x(t)\\ &=e^{\Delta \boldsymbol A}\times\boldsymbol h(t)+\boldsymbol A^{-1}(e^{\Delta \boldsymbol A}-\boldsymbol I)\boldsymbol B\times x(t)\\ &=e^{\Delta \boldsymbol A}\times\boldsymbol h(t)+(\Delta\boldsymbol A)^{-1}(e^{\Delta \boldsymbol A}-\boldsymbol I)\Delta\boldsymbol B\times x(t)\\ :&=\overline{\boldsymbol A}\boldsymbol h(t)+\overline{\boldsymbol B} x(t) \end{aligned}

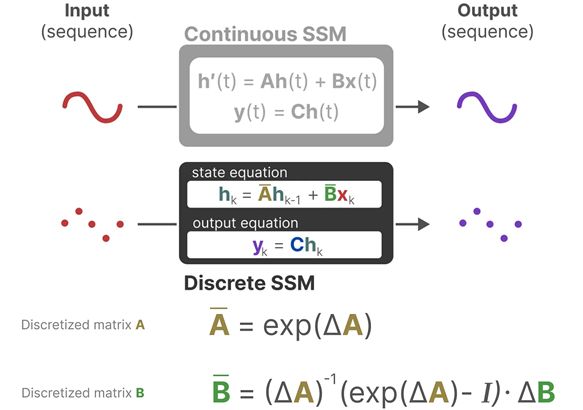
也就是说，考虑离散情况就有：

对比RNN和CNN

离散化之后的SSM由于计算每一个时间步的隐状态变量都需要依靠上一时间步的内容，因此它在结构上是与 循环神经网络 RNN 类似的（如图所示）。

和 RNN 的前向传播过程（见下式）相比，SSM的系数（A‾\overline{A} ,B‾\overline{B} 和CC）涉及到指数运算，由原始的A,B,CA,B,C 得出，并且不使用激活函数。

RNN: h(t)=tanh⁡(Ux(t)+Wh(t−1)+b)SSM: h(t)=A‾h(t−1)+B‾x(t)\begin{aligned} \text{RNN: }&\boldsymbol h^{(t)}=\operatorname{tanh}(\boldsymbol U\boldsymbol x^{(t)}+\boldsymbol W\boldsymbol h^{(t-1)}+\boldsymbol b)\\ \text{SSM: }&\boldsymbol h^{(t)}=\overline{\boldsymbol A}\boldsymbol h^{(t-1)}+\overline{\boldsymbol B}\boldsymbol x^{(t)} \end{aligned}

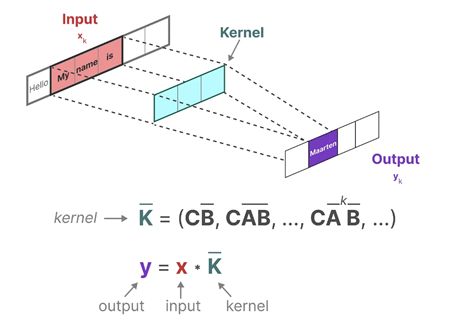
再和 CNN 作对比。如果我们需要计算第kk 个时间步的输出，我们完全可以根据上述递推式一步步计算。但同时，由于A‾\overline{A} ,B‾\overline{B} 和CC （在训练完毕之后）是已知的，所以我们可以将递推关系完全展开书写，在数学上是等价的，即有：

y(k)=(CB‾+CAB‾+⋯+CAkB‾)(x(0)x(1)⋮x(k))y^{(k)}=\big(\boldsymbol C\overline{\boldsymbol B}+\boldsymbol C\overline{\boldsymbol {AB}}+\cdots+\boldsymbol C\overline{\boldsymbol {A}^k\boldsymbol{B}}\big) \begin{pmatrix}\boldsymbol{x}^{(0)}\\\boldsymbol{x}^{(1)}\\\vdots\\\boldsymbol{x}^{(k)}\end{pmatrix}

该过程就可以视为是一维卷积的过程。

由于SSM同时兼具了RNN 和 CNN 的特性，为了高效学习，我们可以在训练SSM时利用卷积模式实现并行计算，而推理（inference）时则利用递归模式对顺序输入依次进行输出。

HiPPO 矩阵

与RNN类似，SSM同样存在难以捕捉长期依赖的问题，这导致模型当前的隐状态只和最近几个时间步的输入强相关，而对更久的输入不再敏感甚至遗忘。

为了解决这个问题，一个有效的方法是“利用多项式函数逼近输入信号”。特别地，这里利用 Orthogonal Polynomials （正交多项式）来在线对输入信号进行投影。

例如，tt 时刻及其之前的历史输入，可以被dd 个多项式Pi(t)P_i(t) 和dd 个系数cic_i 逼近。即：

x≤t(t)≈∑i=1dciPi(t)x_{\leq t}(t)\approx \sum_{i=1}^dc_iP_i(t)

而

ci=∫0tx(τ)Pi(τ)w(τ)dτ∫0tPi2(τ)w(τ)dτc_i=\dfrac{\int_0^t\boldsymbol x(\tau)P_i(\tau)w(\tau)\mathrm d\tau}{\int_0^t P_i^2(\tau)w(\tau)\mathrm d\tau}

式中w(τ)w(\tau) 为权函数。要求多项式Pi(t)P_i(t) 满足两两正交，其中定义在区间(a,b)(a,b) 的多项式正交公式定义如下：

⟨Pi,Pj⟩=∫abPi(x)Pj(x)w(x)  dx\langle P_i,P_j\rangle=\int_a^bP_i(x)P_j(x)w(x)\;\mathrm dx

假设我们取隐状态向量h\boldsymbol h 是用于拟合输入信号x\boldsymbol x 的多项式函数的系数，为了实现系数的在线更新，HiPPO的作者利用状态空间方程来表示这个过程，通过实验最终给出了可以在各种权函数上成立的状态更新矩阵AA 。

HiPPO  Matrix=A=[Ank]={0,n<kn+1,n=k(2n+1)1/2(2k+1)1/2,n>k\mathbf{HiPPO\;Matrix}=\boldsymbol A=[A_{nk}]= \begin{cases} 0,&n\lt k\\ n+1,&n=k\\ (2n+1)^{1/2}(2k+1)^{1/2},&n>k \end{cases}

从而在 S4 中，矩阵AA 初始化为 HiPPO 而不是随机初始化。

HiPPO: Recurrent Memory with Optimal Polynomial Projections (neurips.cc)

矩阵分解

S4 的作者为了更进一步减轻计算开销，还对矩阵进行了 Normal Plus Low-Rank (NPLR) 分解：

A=VΛV∗−PQ⊤=V(Λ−(V∗P)(V∗Q)∗)V∗\boldsymbol{A=V\Lambda V^{*}-PQ^\top=V(\Lambda-(V^*P)(V^*Q)^*)V^*}

无限卷积核

待更

S6: Mamba

Mamba: Linear-Time Sequence Modeling with Selective State Spaces (arxiv.org)

S4 所使用的状态方程原型是一个线性时不变系统，因此这限制了规定 SSM中的三个矩阵A‾\overline{A} ,B‾\overline{B} 和CC 不会因为输入不同而自适应地产生变换，这也导致模型无法针对输入做出侧重点不同的推理。

针对这一问题，Mamba的解决办法是，相比SSM压缩所有历史记录，mamba设计了一个简单的选择机制，通过“函数化SSM的矩阵”，让模型对信息有选择性处理，以便关注或忽略特定的输入。简而言之，就是使得原来的线性时不变系统变为了时变系统。

函数化SSM矩阵

具体来说，Mamba 的作者通过将B,C,ΔB,C,\Delta 三个矩阵都作为以输入为自变量的函数，从而让模型能够根据输入内容自适应地调整其行为。

与 S4 相比，其算法的更改如下：

其中，BB 是批次大小，LL 是序列长度，DD 是输入维度，NN 是隐状态变量的维度。

值得注意的是，此处的AA 看起来形状是 (D,N)，但实际上这是对角化带来的存储压缩优势，在实际计算时，对每一个维度都构建一个N×NN\times N 的对角矩阵用于乘积。再次强调 Mamba 是考虑将每一个维度都视为一个单输入 SSM 来看待，而不是传统线性控制理论中的多输入多输出型线性系统。也因此，所得到的隐状态的形状应该是 (D,N) 。

另外，对于数据驱动的矩阵B,CB,C 来说，并不是直接直接生成 (B,L,D,N) 形状的矩阵，而是线性映射到 (B,L,N) ，后续通过与Δ\Delta 的乘积（广播机制）加上离散化处理得到B‾\overline B，此时的B‾\overline B 就有 D 这个轴了。由于Δ\Delta 也是数据驱动的，所以离散化后的A‾\overline A 也满足了自适应的需求。

对角化矩阵

前面我们提到了对矩阵AA 进行对角化，但是这与 之前提到的 S4 模型中使用的 HiPPO 矩阵似乎不一样。这是因为在 S6:mamba 之前，作者团队的其他一系列文章给出的结论。

待更

并行扫描算法

由于原本训练好后即静态的矩阵都已经被修改成数据依赖的了，这就导致SSM可以无缝转为卷积操作的这种优良特性被打破。因此也就无法利用 CNN 策略实现训练时的并行计算，只能再次遵循 RNN 的模式进行训练。为了在Mamba上实现并行化，作者引入了并行扫描 (parallel scan) 算法使得并行化成为可能。

具体来说，Mamba中的并行扫描算法源于并行计算中经典的并行前缀和(prefix sum)。设输入数组[x0,x1,⋯ ,xn][x_0, x_1,\cdots,x_n] ，定义一个满足分配率的二元操作⊕\oplus 对该数组进行扫描，则算法的输出应该是[x0,x0⊕x1,(x0⊕x1)⊕x2,⋯ ,⨁i=0nxn][x_0,x_0\oplus x_1, (x_0\oplus x_1)\oplus x_2,\cdots, \bigoplus_{i=0}^nx_n]。

很容易得到该算法的一个链式/串式的递归方法：yi←yi−1⊕xiy_i\leftarrow y_{i-1}\oplus x_i，其时间复杂度为O(n)O(n). 而借助分治策略的思想，有效利用二叉树则可以实现一定程度的并行计算。相关的方法有Kogge-Stone算法、Brent-Kung算法、 Hillis-Steele算法和Blelloch算法。其中 Mamba 借鉴的则是 Blelloch 算法。

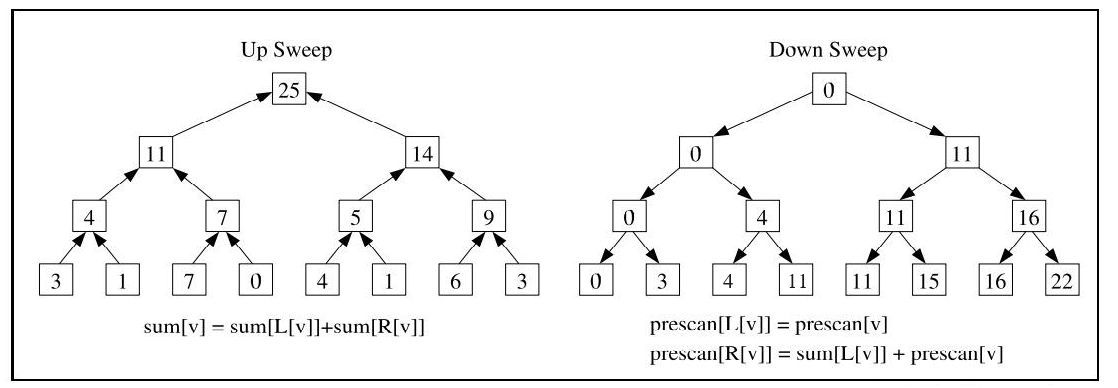
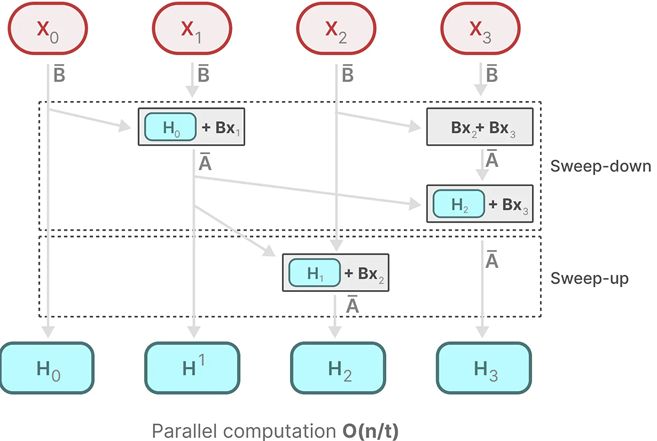
如上图所示，Blelloch 算法主要分为两个阶段：Up-Sweep 和 Down-Sweep。

  • Up-Sweep阶段 ：对nn 个元素中，相邻两个元素两两组合计算累加和，然后将得到的n/2n/2 个结果视为同样的问题进行计算，一直对二叉树进行向上扫描，直到最后得到所有元素的累加和，即根节点。
  • Down-Sweep阶段 ：将根节点置零，然后从根节点开始，向下进行计算：右节点赋值为左节点加上根节点的值，左节点赋值为当前的根节点。计算完毕后，末尾补上上一阶段得到的总的累计和（或者整体左移，去掉开头的0）即可得到输出。

这两个阶段除了总累计和需要一个单位的额外存储，其他的计算都可以在数组内原地计算（见下面的示例），空间复杂度为O(1)O(1)，时间复杂度在理想并行条件的情况下可以达到O(log⁡n)O(\log n) 级。

在 Mamba 中，作者假设执行操作的顺序与关联属性无关。因此，我们可以分段计算序列并迭代地组合。其中定义了⊕\oplus 操作如下：

(A(t),  B(t)x(t))⊕(A(t+!),  B(t+1)x(t+1))=(A(t)A(t+1),  A(t+1)B(t)x(t)+B(t+1)x(t+1))(A^{(t)},\;B^{(t)}x^{(t)})\oplus(A^{(t+!)},\;B^{(t+1)}x^{(t+1)})=(A^{(t)}A^{(t+1)},\;A^{(t+1)}B^{(t)}x^{(t)}+B^{(t+1)}x^{(t+1)})

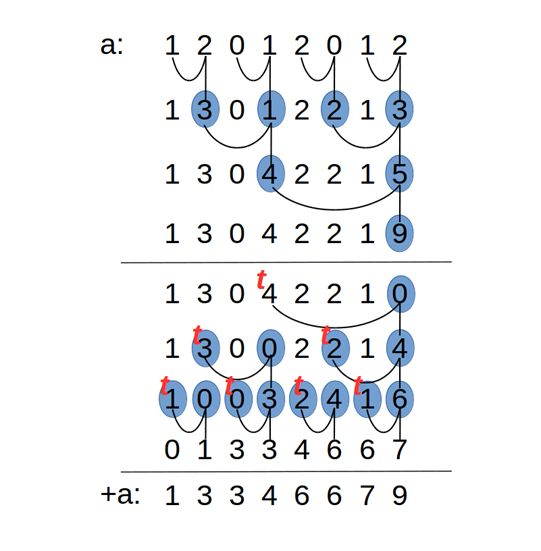
使用 Blelloch 算法实现并行。如下图所示：

如果令 执行任务的处理器或计算单元的数量 为tt ，则时间复杂度可降到O(n/t)O(n/t)。

相关链接：

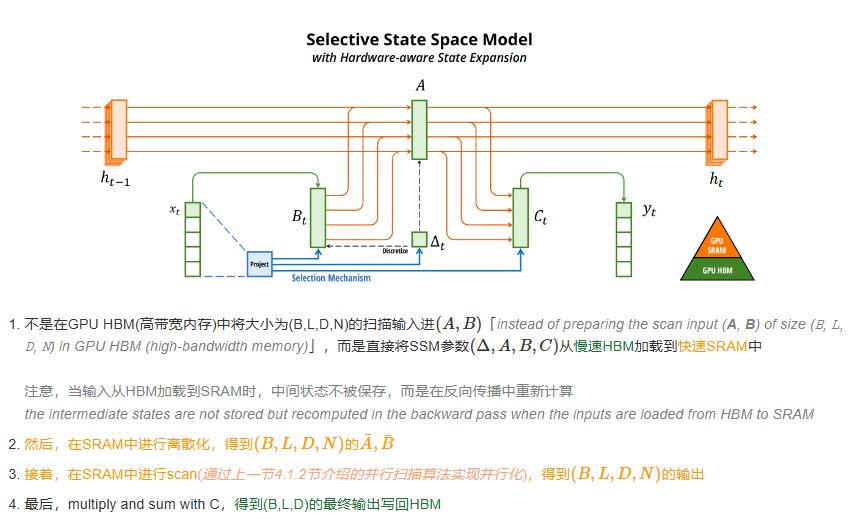
  1. 第十一章：前缀扫描 - 李理的博客
  2. Hillis Steele Scan(并行前缀扫描算法) | 码农参考
  3. NVIDIA CUDA 高度并行处理器编程（七）：并行模式：前缀和_cuda前缀和-CSDN博客
  4. Mamba.py：扫描和并行扫描 - 知乎
  5. CUDA-扫描算法 | Junhui’s Journal (ashburnlee.github.io)

硬件感知设计

另一方面，为了让传统的 SSM 在现代 GPU 上也能高效计算，Mamba还沿用了其作者之前的论文中所介绍的Flash Attention技术。具体而言就是限制需要从 DRAM 到 SRAM 的次数(通过内核融合kernel fusion来实现)，避免一有个结果便从SRAM写入到DRAM，而是待SRAM中有一批结果再集中写入DRAM中，从而降低来回读写的次数。在更高速的SRAM内存中执行离散化和递归操作，再将输出写回HBM（(high-bandwidth memory）。

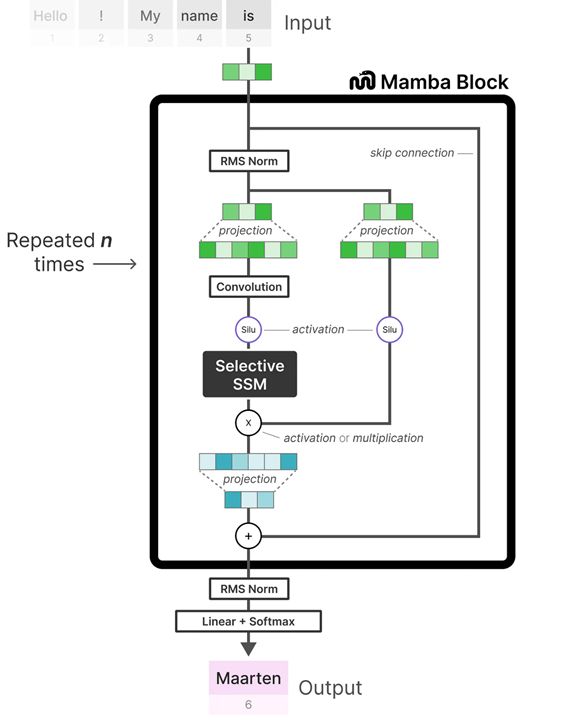
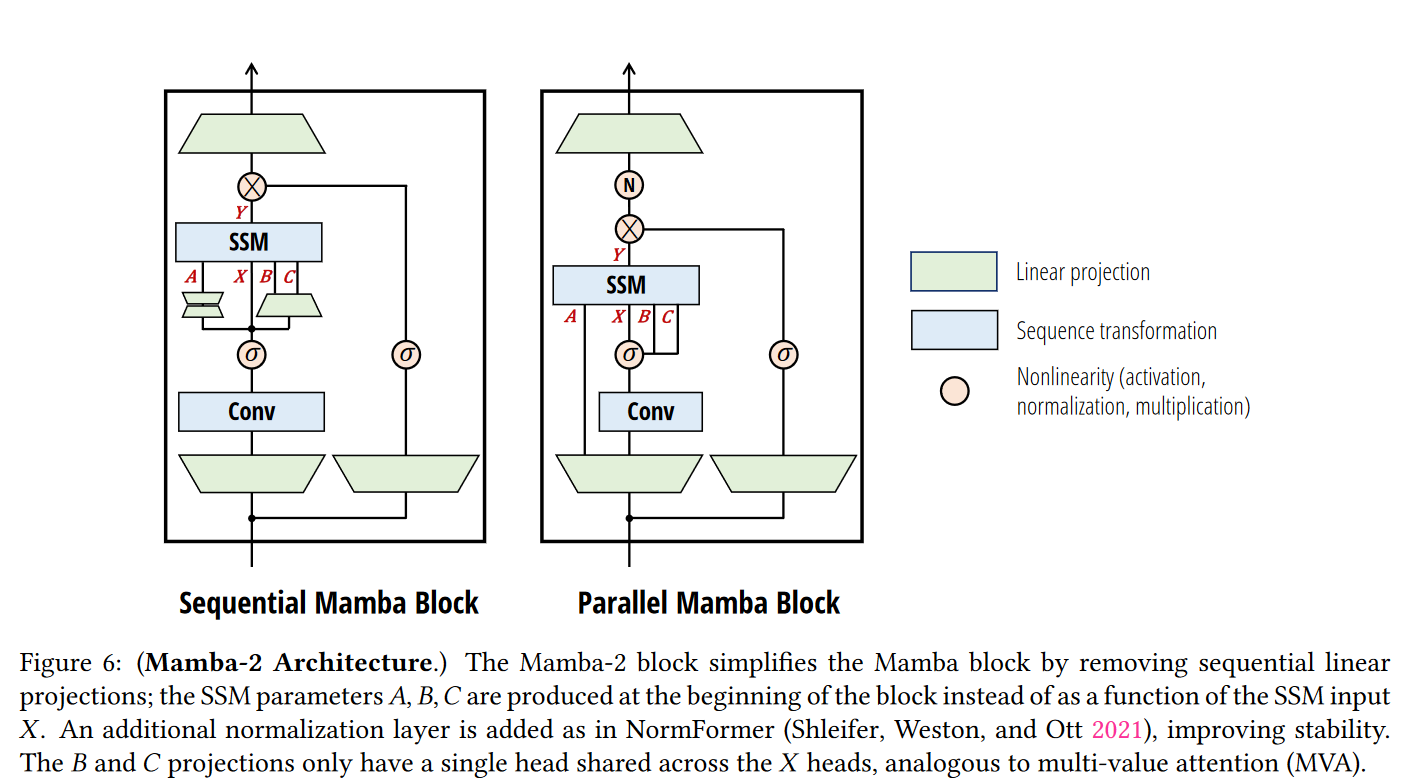
Mamba Block

将大多数 SSM 架构比如 H3 的基础块，与现代神经网络比如 Transformer 中普遍存在的门控MLP相结合，组成新的Mamba块，重复这个块，与归一化和残差连接(相当于原来的DD 矩阵) 结合，便构成了Mamba架构，如下图所示。

其中，线性投影层（Projection）将输入的 embedding 的维度进行调整（通常是增大维度），以便让模型能够处理更高维度的特征空间，从而捕获更细致、更复杂的特征。而后经过的 卷积层（Convolution） 则负责提取局部的短距离特征（此处是1维卷积），与之后负责捕捉长期依赖的SSM互为补充，确保在进入 SSM 之前，序列中的每个 token 已经考虑到了其相邻 token 的信息，解决了模型单独地处理每个 token，而没有考虑了局部上下文的问题。

SSD: Mamba2

Paper：Transformers are SSMs: Generalized Models and Efficient Algorithms Through Structured State Space Duality
官方博客：Blog | Tri Dao

Mamba 的出现似乎抓住了连续系统、卷积网络和循环神经网络的本质，但是在它在概念层面上仍然与如今序列模型大规模使用的变体注意力机制有所脱节，不仅如此，从计算的角度来看，它的硬件效率仍然远低于注意力等机制。

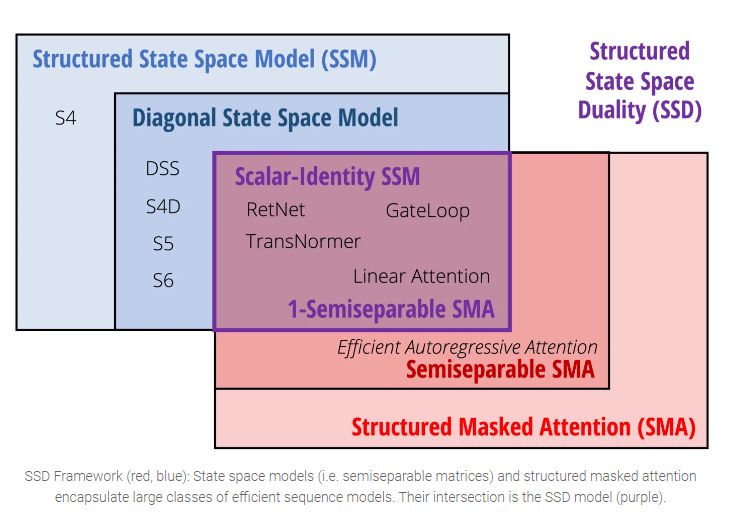
为了解决以上问题，Mamba的作者进一步提出了结构化状态空间对偶 （structured state space duality，SSD）的概念，包括 作为神经网络构建的SSD Model、在理论上推导SSM和Attention关系的 SSD Framework 和 用于高效计算的 SSD Algorithm。

SSD层的前向计算

与 Mamba-1 相比，SSD Layer 直接做了减法，令原本需要NN 个存储空间的对角矩阵A∈RN×N\mathbf A\in\mathbb R^{N\times N} 中所有的NN 个对角元素都为相同的值，从而在tt 时刻的对角矩阵只需要一个标量a(t)a^{(t)} 即可存储，这个改动被称为 scalar-times-identity structure onA\bf A。

而对与DD 维的多输入，正如前文所说，Mamba 对每一个通道都做一个单值输入SSM，而作者在这里将这种操作类比多头注意力，给出了 多头SSM 的说法。在这种语境下维度DD 也就是多头的个数。最终，我们得到一个 SSM Layer 的全局表达：

Y(T,D)=SSM(A(T,…),B(T,N),C(T,N))(X(T,D))\mathbf Y^\mathtt{(T,D)} = \mathsf{SSM}(\mathbf A^\mathtt{(T,…)}, \mathbf B^\mathtt{(T,N)}, \mathbf C^\mathtt{(T,N)})(\mathbf X^\mathtt{(T,D)})

这里的上标表示的是数据的尺寸形状，如Y(T,D)\mathbf Y^\mathtt{(T,D)} 表示模型的输出Y∈RT×D\mathbf Y\in\mathbb R^{T\times D} ，其中TT 是输入序列的长度（也就是时间步的数量），DD 表示输入/输出维度，也就是 SSM 的头部数量。

注意，A,B,C\bf A,B,C 的尺寸都会在后续离散化和计算时进行扩张，上面这个表达式的上标仅仅是对数据存储而言

当表达式中的 (...) 不同时，代表不同类型的 SSM：

  • ... = (N,N) 对应的就是传统的 SSM
  • ... = (N)对应的就是对角化的 SSM（或其他结构化SSM，例如对角矩阵分解）
  • ... = () 对应的就是 SSD

特别地，如果令矩阵L∈R(T,T)\mathbf L\in\mathbb R^{\mathtt{(T,T)}} 如下：

L=[1a11a2a1a21⋮⋮⋱⋱aT−1…a1aT−1…a2…aT−11]\mathbf L = \begin{bmatrix} 1 & \\ a_1 & 1 & \\ a_2a_1 & a_2 & 1 \\ \vdots & \vdots & \ddots & \ddots \\ a_{\mathtt{T}-1}\dots a_1 & a_{\mathtt{T}-1}\dots a_2 & \dots & a_{\mathtt{T}-1} & 1 \\ \end{bmatrix}

再定义矩阵M\mathbf M 如下：

M=L∘CB⊤∈R(T,T)\mathbf M = \mathbf L \circ \mathbf{C B}^\top \in \mathbb{R}^{\mathtt{(T,T)}}

那么，这样的一个矩阵就是在单个SSM头下的序列变换x∈R(T)→y∈R(T)\boldsymbol x\in\mathbb R^{\mathtt{(T)}}\to\boldsymbol y\in\mathbb R^{\mathtt{(T)}}.
从而可以直接用y=Mx\boldsymbol y=\mathbf M\boldsymbol x 来代表一个SSD的前向计算过程。

有趣的是，如果令L\mathbf L 矩阵中的at=1a_t=1，那么L\mathbf L 就成了一个简单的下三角因果掩码（lower-triangular causal mask），于是上式与因果线性注意力（causal linear attention）的公式就完全一致了！仅仅只是变量名不同而已！

Y=(L∘QK⊤)V\mathbf Y = (\mathbf L \circ \mathbf{Q K}^\top)\mathbf V

所谓的对偶性就是指原来遵循RNN模式的 SSM 前向可以“对偶”地表达成和注意力机制相似的矩阵乘法形式。

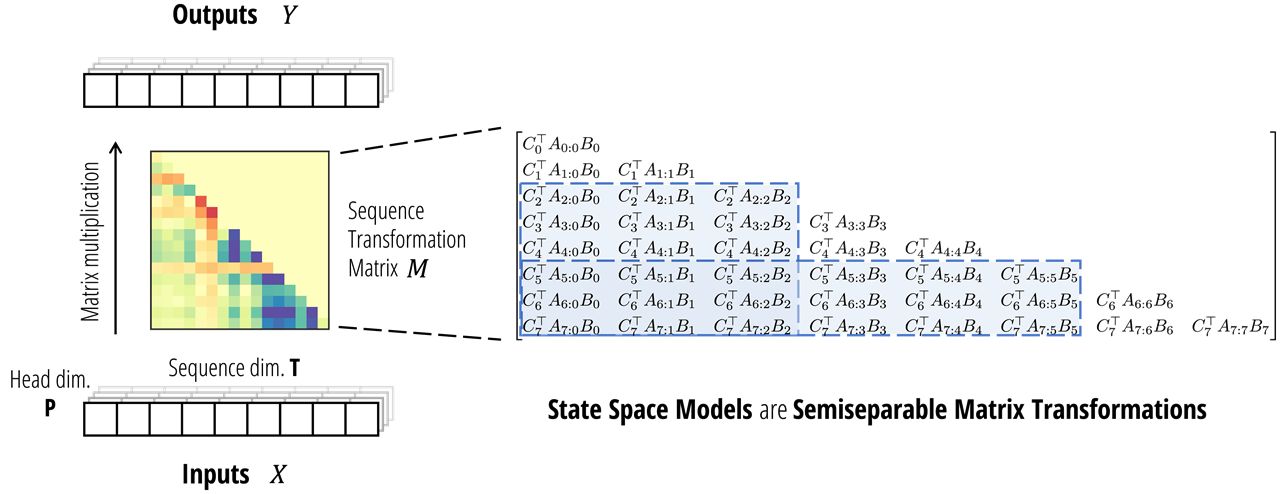
可见，scalar-times-identity structure on A\bf A 的这个简单的改动使得 SSM 的计算可以适用于矩阵乘法，这虽然会略微降低表达能力，但却显著提高了训练效率，特别是允许在现代加速器上使用矩阵乘法单元。

状态空间对偶框架

本节将证明为什么 SSM 的计算过程可以表示成矩阵变换的形式，以及该形式和注意力机制的联系，最终外推和泛化，总结了 SSM 和 Transformer 的关联，从而提出 SSD Framework。

SSM 角度的理解

与传统 RNN 的非线性计算不同，考虑单个头的前向过程y=SSM(A,B,C)(x)\boldsymbol y = \mathsf{SSM}(\mathbf A, \mathbf B, \mathbf C)(\boldsymbol x) ，它总可以表示成y=Mx\boldsymbol y=\mathbf M\boldsymbol x 的形式，其中M\bf M 展开可以写成：

[C0⊤B0C1⊤A1B0C1⊤B1C2⊤A2A1B0C2⊤A2B1C2⊤B2⋮⋮⋱⋱CT⊤AT−1…A1B0CT⊤AT−1…A2B1…CT⊤AT−1BT−2CT⊤BT−1]\begin{bmatrix} C_0^\top B_0 & \\ C_1^\top A_1 B_0 & C_1^\top B_1 & \\ C_2^\top A_2A_1 B_0 & C_2^\top A_2 B_1 & C_2^\top B_2 \\ \vdots & \vdots & \ddots & \ddots \\ C_\mathtt{T}^\top A_{\mathtt{T}-1}\dots A_1 B_0 & C_\mathtt{T}^\top A_{\mathtt{T}-1}\dots A_2 B_1 & \dots & C_\mathtt{T}^\top A_{\mathtt{T}-1} B_{\mathtt{T}-2} & C_\mathtt{T}^\top B_{\mathtt{T}-1} \\ \end{bmatrix}

显然它是一个下三角矩阵，当i<ji < j 时，Mij=0M_{ij} = 0；否则

Mij=Ci⊤Ai:j×Bj:=Ci⊤Ai…Aj+1BjM_{ij} = C_i^\top A_{i:j}^\times B_j := C_i^\top A_i \dots A_{j+1} B_j

实际上，M\bf M 的结构符合（三角）半可分离(Semiseparable) 矩阵，这类矩阵已经在工程和计算线性代数的其他领域进行了研究。

定义：一个(下)三角矩阵称为 N-semiseparable ，当且仅当其严格下三角部分(即下三角部分去掉对角线)的任意子矩阵的秩不超过NN 。这里的NN 称为semiseparable矩阵的阶或秩。

Semiseparable矩阵的一个重要性质就是虽然完整矩阵有O(T2)O(T^2) 个元素，但其SSS表示只需O(NT)O(NT) 的参数，且在这个表示上可以实现矩阵乘法等基本操作的近似线性时间算法。因此，所有用于计算状态空间模型的算法都可以看作是Semiseparable矩阵上的结构化矩阵乘法算法，反过来也可以用已有的对Semiseparable矩阵的算法作用在 SSM 上。

当 scalar-times-identity structure on A\bf A 时，就得到：

Ci⊤Ai:j×Bj=Ai:j×⋅(Ci⊤Bj)C_i^\top A_{i:j}^\times B_j = A_{i:j}^\times \cdot (C_i^\top B_j)

从而导出M=L∘CB⊤\mathbf M = \mathbf L \circ \mathbf{C B}^\top.

Attention 角度的理解

在 Transformer 中，Self Attention 层作为主要部件占用了较大的计算复杂度。回顾其计算公式：

softmax⁡(QK⊤d)V\begin{aligned} \operatorname{softmax}\left(\frac{QK^\top }{\sqrt{d}}\right)V \end{aligned}

其中的QK⊤QK^\top 作矩阵乘法时，会产生O(T2)O(T^2) 的复杂度，TT 为是矩阵Q,KQ,K 行数，在自注意力机制中实际的物理含义是输入序列个数。

如今已经有很多研究尝试将注意力机制的二次复杂性计算代价降到线性。在Mamba2中，作者沿用了 《Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention》的思路，尝试用更一般的形式来刻画注意力机制，即对于任何Y=f(QK⊤)⋅VY = f(QK^\top) \cdot V ，而不是仅仅讨论 Softmax 自注意力。

如下所示：

Y=f(QK⊤)⋅V=ψ(Q)ψ(K)⊤⋅VLet Q←ψ(Q),  K←ψ(K)then Y=(QK⊤)⋅V\begin{aligned} Y&=f(QK^\top)\cdot V\\ &=\psi(Q)\psi(K)^\top\cdot V\\\\ \text{Let } Q&\leftarrow\psi(Q),\;K\leftarrow\psi(K)\\ \text{then }Y&=(QK^\top)\cdot V \end{aligned}

上式的结果还可以进一步通过矩阵乘积的结合律将计算降到线性，即Y=Q⋅(K⊤V)Y=Q\cdot (K^\top V).

但是，如果考虑带掩码的注意力机制（设掩码矩阵为LL ）就有：

Y=(L∘QK⊤)⋅VY = (L \circ Q K^\top)\cdot V

这使得问题变得复杂，不再能使用结合律以降低复杂度。不过 Mamba2 的作者通过理论推导，得出任意带掩码的注意力机制，都可以表示为4个张量的缩并(Contraction)。从而得到具有线性复杂度的表达式：

Y=Q⋅cumsum(K⊤V)Y = Q \cdot \mathsf{cumsum}(K^\top V)

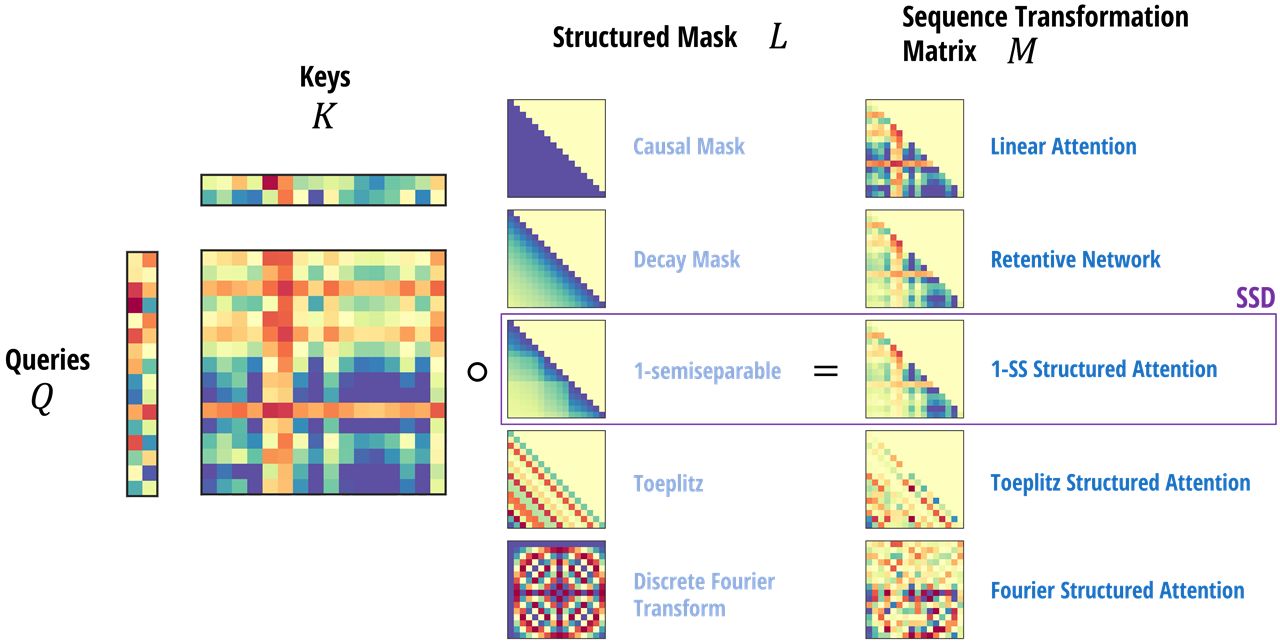
最终，作者提出了 Structured masked attention (SMA) 结构化掩码注意力的模型。显然，该模型具有二次复杂度的版本，也有线性版本，并且二次形式的版本和 SSD 的表达式是同构的！注意力机制中重命名(Q,K,V)↦(C,B,X)(Q,K,V)\mapsto (C,B,X) 正好对应了 SSM 中的矩阵，并且他们同样都是通过Linear\texttt{Linear} 层得来的，甚至也都是多头的，唯一的不同可能就是掩码矩阵LL 不同——可以认为当线性注意力的掩码矩阵是一个下三角的Semiseparable矩阵时，它就是SSM。

SSM vs. Attention

如下图所示，当SSM的矩阵AA 使用对角矩阵，并且更进一步采用单标量；当SMA的掩码矩阵使用半可分离矩阵，并且更进一步采用1阶半可分离矩阵时，他们二者是等价的。

矩阵分块算法

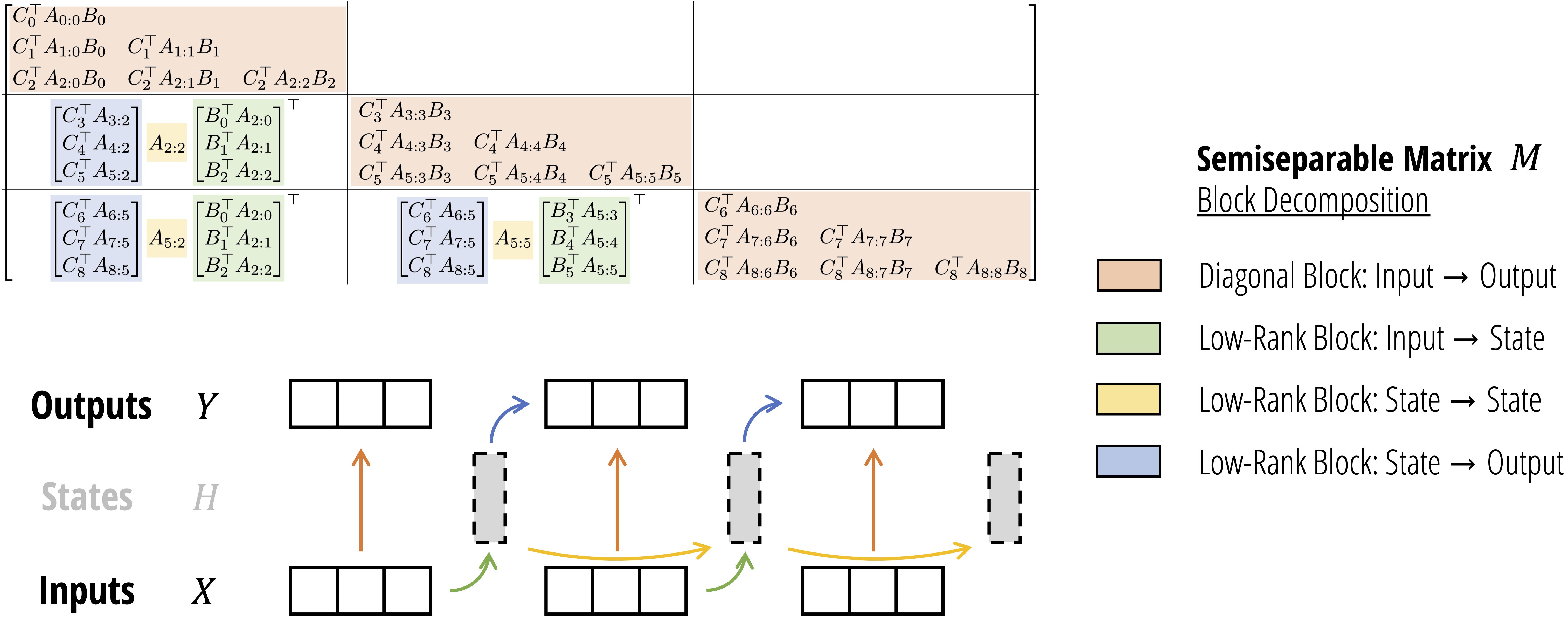
Mamba-2 为了利用GPU的 Tensor Core 实现高效的矩阵乘法，首先将半可分离的 SSM 矩阵划分为大小为 Q×Q 的块，然后，利用Semiseparable矩阵的性质来分解每个低秩的非对角块：

  1. （橙色）每个对角块是一个更小的半可分矩阵，可以以喜欢的方式计算这个乘法，特别是使用 SSD 的二次（类似注意力机制）形式。
  2. （绿色）总共有 T/Q 个不同的绿色块，通过批处理矩阵乘法来计算。
  3. （黄色）注意，黄色项本身是一个 1 - 半可分矩阵，这一步等价于对某些修改后的 A 因子的 SSM 扫描。
  4. （蓝色）与绿色类似，通过批处理矩阵乘法来计算。

Mamba2的架构

与 Mamba-1 相比，Mamba-2 的 SSD层 被视为(A，X，B，C)↦Y(A，X，B，C)\mapsto Y 的映射，因此，类比注意力机制，可以直接在块的开头直接用单个投影并行地产生A,X,B,CA,X,B,C 而不是像之前一样将B,CB,C 视为XX 的函数进行线性投影。

除此之外，作者进行多个预实验得出，当模型规模较大时容易出现不稳定的现象，最后通过在输出投影之前添加一个额外的归一化层 ( 比如 LayerNorm、GroupNorm或 RMSNorm)来缓解这个问题。

值得注意的是，作者表示对于 Mamba 来说，对矩阵进行离散化可能是不必要的，离散化是沿用以前 SSM 的传统，但是以现代视角来看，或许可以直接使用参数化的矩阵即可。当然，在代码中，还是提供了对应的可选项供用户选择。

代码梳理

代码截取时间：2024年9月18日14:40:51

mamba.py

官方源代码：mamba_simple.py · state-spaces/mamba
直接实现：alxndrTL/mamba.py
极简实现：johnma2006/mamba-minimal

Github 中有三种 mamba 的实现。官方实现中目录层级较多，并且利用 C 语言 实现了各种优化和加速。此外，有第三方实现直接在Pytorch上进行优化加速，特别是对并行扫描算法的加速。最后是一个极简实现，致力用一个文件实现所有的核心算法，速度也是最慢了，适合用作教学。

本节将采用第二个仓库的代码进行适当的梳理和解析。

1
2
3
4
5
6
7
8
9
import math
from dataclasses import dataclass
from typing import Union

import torch
import torch.nn as nn
import torch.nn.functional as F

from mambapy.pscan import pscan #自实现的并行扫描，后续讲解

ModelArgs 类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

# 使用dataclass装饰器自动生成初始化方法和类的字符串表示方法
@dataclass
class MambaConfig:
    d_model: int # D
    n_layers: int
    dt_rank: Union[int, str] = 'auto' # Δ的秩，对应Mamba论文中3.6节的“parameterization of Δ”
    d_state: int = 16 # 每个输入特征的状态向量维度，Mamba论文中的`N`
    expand_factor: int = 2 # 扩张系数，Mamba论文3.4节的`E`
    d_conv: int = 4 # 1d卷积核大小

    dt_min: float = 0.001
    dt_max: float = 0.1
    dt_init: str = "random" # "random" or "constant"
    dt_scale: float = 1.0
    dt_init_floor = 1e-4

    rms_norm_eps: float = 1e-5
    base_std: float = 0.02

    bias: bool = False
    conv_bias: bool = True
    inner_layernorms: bool = False # apply layernorms to internal activations

    mup: bool = False
    mup_base_width: float = 128 # width=d_model

    pscan: bool = True # 使用并行扫描 parallel scan mode 或者顺序扫描 sequential mode
    use_cuda: bool = False # 使用官方的 CUDA 实现方案 (not compatible with (b)float16)

	# __post_init__() 在 __init__() 后自动被调用
    def __post_init__(self):
		# 计算内部维度，即扩展后的维度. 即 E*D
        self.d_inner = self.expand_factor * self.d_model

        if self.dt_rank == 'auto':
		    # 根据隐藏层维度自动计算Δ的秩
            self.dt_rank = math.ceil(self.d_model / 16)

        # muP
        if self.mup:
            self.mup_width_mult = self.d_model / self.mup_base_width

MambaBlock 类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
class MambaBlock(nn.Module):
    def __init__(self, config: MambaConfig):
        super().__init__()

        self.config = config
		
        # projects block input from D to 2*ED (two branches)
        # 内部计算时维度都是 d_inner，这里一次性投影两份，另一份用于后续的跳接
        self.in_proj = nn.Linear(config.d_model, 2 * config.d_inner, bias=config.bias)

        self.conv1d = nn.Conv1d(in_channels=config.d_inner, out_channels=config.d_inner, 
                              kernel_size=config.d_conv, bias=config.conv_bias, 
                              groups=config.d_inner,
                              padding=config.d_conv - 1)
        
        # projects x to input-dependent delta, B, C
        # 一次性投影3份，得到 delta, B, C
        self.x_proj = nn.Linear(config.d_inner, config.dt_rank + 2 * config.d_state, bias=False)

        # projects delta from dt_rank to d_inner
        # 前面将 delta 进行低秩投影，需要再投影回应该有的维度大小
        self.dt_proj = nn.Linear(config.dt_rank, config.d_inner, bias=True)

        # dt initialization
        # dt weights
        dt_init_std = config.dt_rank**-0.5 * config.dt_scale
        if config.dt_init == "constant":
            nn.init.constant_(self.dt_proj.weight, dt_init_std)
        elif config.dt_init == "random":
            nn.init.uniform_(self.dt_proj.weight, -dt_init_std, dt_init_std)
        else:
            raise NotImplementedError
        
        # delta bias
        dt = torch.exp(
            torch.rand(config.d_inner) * (math.log(config.dt_max) - math.log(config.dt_min)) + math.log(config.dt_min)
        ).clamp(min=config.dt_init_floor)
        inv_dt = dt + torch.log(-torch.expm1(-dt)) # inverse of softplus: https://github.com/pytorch/pytorch/issues/72759
        with torch.no_grad():
            self.dt_proj.bias.copy_(inv_dt)
        #self.dt_proj.bias._no_reinit = True # initialization would set all Linear.bias to zero, need to mark this one as _no_reinit
        # todo : explain why removed

        # S4D real initialization
        # A矩阵初始化为 d_inner 行的 [1,2,...]，并且以对数值存储，后续再指数计算回来，原因见后续的论述
        A = torch.arange(1, config.d_state + 1, dtype=torch.float32).repeat(config.d_inner, 1)
        self.A_log = nn.Parameter(torch.log(A))
        self.A_log._no_weight_decay = True

        self.D = nn.Parameter(torch.ones(config.d_inner))
        self.D._no_weight_decay = True

        # projects block output from ED back to D
        # 从 d_inner 投影回输出维度
        self.out_proj = nn.Linear(config.d_inner, config.d_model, bias=config.bias)

        # used in jamba
        if self.config.inner_layernorms:
            self.dt_layernorm = RMSNorm(self.config.dt_rank, config.rms_norm_eps, config.mup)
            self.B_layernorm = RMSNorm(self.config.d_state, config.rms_norm_eps, config.mup)
            self.C_layernorm = RMSNorm(self.config.d_state, config.rms_norm_eps, config.mup)
        else:
            self.dt_layernorm = None
            self.B_layernorm = None
            self.C_layernorm = None

        if self.config.use_cuda:
            try:
                from mamba_ssm.ops.selective_scan_interface import selective_scan_fn
                self.selective_scan_cuda = selective_scan_fn
            except ImportError:
                print("Failed to import mamba_ssm. Falling back to mamba.py.")
                self.config.use_cuda = False
                
    def _apply_layernorms(self, dt, B, C):
        if self.dt_layernorm is not None:
            dt = self.dt_layernorm(dt)
        if self.B_layernorm is not None:
            B = self.B_layernorm(B)
        if self.C_layernorm is not None:
            C = self.C_layernorm(C)
        return dt, B, C

    def forward(self, x):
        # x : (B, L, D)
        
        # y : (B, L, D)

        _, L, _ = x.shape

        xz = self.in_proj(x) # (B, L, 2*ED)
        x, z = xz.chunk(2, dim=-1) # (B, L, ED), (B, L, ED)

        # x branch
        # 先调整x的轴的位置(即形状 shape) 以适应 conv1d
        # 然后深度卷积后截取前L个输出，最后又将x的形状调整回来
        x = x.transpose(1, 2) # (B, ED, L)
        x = self.conv1d(x)[:, :, :L] # depthwise convolution over time, with a short filter
        x = x.transpose(1, 2) # (B, L, ED)

        x = F.silu(x)
        y = self.ssm(x, z)

        if self.config.use_cuda:
            output = self.out_proj(y) # (B, L, D)
            return output # the rest of the operations are done in the ssm function (fused with the CUDA pscan)

        # z branch
        z = F.silu(z)

        output = y * z
        output = self.out_proj(output) # (B, L, D)

        return output
    
    def ssm(self, x, z):
        # x : (B, L, ED)

		# 将 A_log 通过指数运算还原出来
        A = -torch.exp(self.A_log.float()) # (ED, N)
        D = self.D.float()

		# 分离出三个参数 delta, B, C
        deltaBC = self.x_proj(x) # (B, L, dt_rank+2*N)
        delta, B, C = torch.split(deltaBC, [self.config.dt_rank, self.config.d_state, self.config.d_state], dim=-1) # (B, L, dt_rank), (B, L, N), (B, L, N)
        delta, B, C = self._apply_layernorms(delta, B, C)
        
        # 将低秩投影的 delta 投影到应该有的维度大小
        delta = self.dt_proj.weight @ delta.transpose(1, 2) # (ED, dt_rank) @ (B, L, dt_rank) -> (B, ED, L)
        # here we just apply the matrix mul operation of delta = softplus(dt_proj(delta))
        # the rest will be applied later (fused if using cuda)
        

        if self.config.use_cuda:
            # these are unfortunately needed for the selective_scan_cuda function
            x = x.transpose(1, 2)
            B = B.transpose(1, 2)
            C = C.transpose(1, 2)
            z = z.transpose(1, 2)

            # "softplus" + "bias" + "y * silu(z)" operations are fused
	        # 此处借用官方实现以进行数据融合
            y = self.selective_scan_cuda(x, delta, A, B, C, D, z=z, delta_softplus=True, delta_bias=self.dt_proj.bias.float())
            y = y.transpose(1, 2) # (B, L, ED)
        
        else:
            delta = delta.transpose(1, 2)
            delta = F.softplus(delta + self.dt_proj.bias)

            if self.config.pscan:
                y = self.selective_scan(x, delta, A, B, C, D)
            else:
                y = self.selective_scan_seq(x, delta, A, B, C, D)

        return y

	# 自实现的并行扫描
    def selective_scan(self, x, delta, A, B, C, D):
        # x : (B, L, ED)
        # Δ : (B, L, ED)
        # A : (ED, N)
        # B : (B, L, N)
        # C : (B, L, N)
        # D : (ED)

        # y : (B, L, ED)

        deltaA = torch.exp(delta.unsqueeze(-1) * A) # (B, L, ED, N)
        deltaB = delta.unsqueeze(-1) * B.unsqueeze(2) # (B, L, ED, N)

        BX = deltaB * (x.unsqueeze(-1)) # (B, L, ED, N)
        
        hs = pscan(deltaA, BX)

        y = (hs @ C.unsqueeze(-1)).squeeze(3) # (B, L, ED, N) @ (B, L, N, 1) -> (B, L, ED, 1)

        y = y + D * x

        return y

	# 自实现的顺序扫描
    def selective_scan_seq(self, x, delta, A, B, C, D):
        # x : (B, L, ED)
        # Δ : (B, L, ED)
        # A : (ED, N)
        # B : (B, L, N)
        # C : (B, L, N)
        # D : (ED)

        # y : (B, L, ED)

        _, L, _ = x.shape

        deltaA = torch.exp(delta.unsqueeze(-1) * A) # (B, L, ED, N)
        deltaB = delta.unsqueeze(-1) * B.unsqueeze(2) # (B, L, ED, N)

        BX = deltaB * (x.unsqueeze(-1)) # (B, L, ED, N)

        h = torch.zeros(x.size(0), self.config.d_inner, self.config.d_state, device=deltaA.device) # (B, ED, N)
        hs = []

        for t in range(0, L):
            h = deltaA[:, t] * h + BX[:, t]
            hs.append(h)
            
        hs = torch.stack(hs, dim=1) # (B, L, ED, N)

        y = (hs @ C.unsqueeze(-1)).squeeze(3) # (B, L, ED, N) @ (B, L, N, 1) -> (B, L, ED, 1)

        y = y + D * x

        return y

# -------------------------- inference -------------------------- #
    def step(self, x, cache):
	    # 该步骤用于缓存输入和状态变量，以便在推理时使用
        # x : (B, D)
        # cache : (h, inputs)
                # h : (B, ED, N)
                # inputs : (B, ED, d_conv-1)
        
        # y : (B, D)
        # cache : (h, inputs)
        
        h, inputs = cache
        
        xz = self.in_proj(x) # (B, 2*ED)
        x, z = xz.chunk(2, dim=1) # (B, ED), (B, ED)

        # x branch
        x_cache = x.unsqueeze(2)
        x = self.conv1d(torch.cat([inputs, x_cache], dim=2))[:, :, self.config.d_conv-1] # (B, ED)

        x = F.silu(x)
        y, h = self.ssm_step(x, h)

        # z branch
        z = F.silu(z)

        output = y * z
        output = self.out_proj(output) # (B, D)

        # prepare cache for next call
        inputs = torch.cat([inputs[:, :, 1:], x_cache], dim=2) # (B, ED, d_conv-1)
        cache = (h, inputs)
        
        return output, cache

    def ssm_step(self, x, h):
        # x : (B, ED)
        # h : (B, ED, N)

        # y : (B, ED)
        # h : (B, ED, N)

        A = -torch.exp(self.A_log.float()) # (ED, N) 
        D = self.D.float()

        deltaBC = self.x_proj(x) # (B, dt_rank+2*N)

        delta, B, C = torch.split(deltaBC, [self.config.dt_rank, self.config.d_state, self.config.d_state], dim=-1) # (B, dt_rank), (B, N), (B, N)
        delta, B, C = self._apply_layernorms(delta, B, C)
        delta = F.softplus(self.dt_proj(delta)) # (B, ED)

        deltaA = torch.exp(delta.unsqueeze(-1) * A) # (B, ED, N)
        deltaB = delta.unsqueeze(-1) * B.unsqueeze(1) # (B, ED, N)

        BX = deltaB * (x.unsqueeze(-1)) # (B, ED, N)

        if h is None:
            h = torch.zeros(x.size(0), self.config.d_inner, self.config.d_state, device=deltaA.device) # (B, ED, N)

        h = deltaA * h + BX # (B, ED, N)

        y = (h @ C.unsqueeze(-1)).squeeze(2) # (B, ED, N) @ (B, N, 1) -> (B, ED, 1)

        y = y + D * x

        return y, h

关于代码中的矩阵AA 为什么采用 A_log 的形式进行初始化和参数化？

作者在 Issue #326 给出的解释是，追溯到数字信号处理领域的知识，认为一个对角阵的元素值全负，其特征值也就全负，这意味着该系统为有界输入且有界输出的稳定系统。也就是说不期望隐状态变量爆炸，否则会导致梯度消失问题。当对初始化元素全部取 torch.log() 之后再 -torch.exp(A_log) 回来，可以保证参数AA 始终为负。类似地，利用 delta = softplus(dt + self.dt_bias) 可以让参数Δ\Delta 始终保持为正。

关于代码中的矩阵BB 为什么在代码中没有遵循论文里通过零阶保持(ZOH)推导的公式？

作者在 Issue #19 和 Issue #114 指出，为了计算方便，它们直接把原来的Bˉ=(ΔA)−1(exp⁡(ΔA)−I)⋅ΔB\bar{B}=(\Delta A)^{-1}(\exp(\Delta A)-I)\cdot\Delta B 在代码里使用Bˉ=ΔB\bar{B}=\Delta B 代替了。其实这是因为运用了一阶近似，即欧拉近似（the Euler approximation）。具体来说，就是常见的ex−1∼xe^x-1\sim x .

ResidualBlock 类

A ResidualBlock is composed of a MambaBlock, a normalization, and a residual connection : ResidualBlock(x) = mamba(norm(x)) + x
This leaves us with the MambaBlock : its input x is (B, L, D) and its outputs y is also (B, L, D).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class ResidualBlock(nn.Module):
    def __init__(self, config: MambaConfig):
        super().__init__()

        self.mixer = MambaBlock(config)
        self.norm = RMSNorm(config.d_model, config.rms_norm_eps, config.mup)

    def forward(self, x):
        # x : (B, L, D)

        # output : (B, L, D)

        output = self.mixer(self.norm(x)) + x
        return output
    
    def step(self, x, cache):
        # x : (B, D)
        # cache : (h, inputs)
                # h : (B, ED, N)
                # inputs: (B, ED, d_conv-1)

        # output : (B, D)
        # cache : (h, inputs)

        output, cache = self.mixer.step(self.norm(x), cache)
        output = output + x
        return output, cache

# 补充：RMSNorm的实现
class RMSNorm(nn.Module):
    def __init__(self, d_model: int, eps: float = 1e-5, use_mup: bool = False):
        super().__init__()

        self.use_mup = use_mup
        self.eps = eps

        # https://arxiv.org/abs/2404.05728, RMSNorm gains prevents muTransfer (section 4.2.3)
        if not use_mup:
            self.weight = nn.Parameter(torch.ones(d_model))

    def forward(self, x):
        output = x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)

        if not self.use_mup:
            return output * self.weight
        else:
            return output

Mamba 类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Mamba(nn.Module):
    def __init__(self, config: MambaConfig):
        super().__init__()

        self.config = config

        self.layers = nn.ModuleList([ResidualBlock(config) for _ in range(config.n_layers)])

    def forward(self, x):
        # x : (B, L, D)
        for layer in self.layers:
            x = layer(x)

        return x
    
    def step(self, x, caches):
        # x : (B, L, D)
        # caches : [cache(layer) for all layers], cache : (h, inputs)

        for i, layer in enumerate(self.layers):
            x, caches[i] = layer.step(x, caches[i])

        return x, caches

mamba2.py

官方源代码：mamba2_simple.py · state-spaces/mamba
直接实现：alxndrTL/mamba.py
极简实现：tommyip/mamba2-minimal

Mamba 第二代同样有第三方实现，其中第二个“直接实现”截止写下这篇博客时还未完善，这里我们采用第三个仓库的版本进行整理。

该版本代码以语言模型（language model, lm）为背景而编写，所以有些许针对性的代码。另外，为简洁，下面的梳理注释中仅保留与 Mamba 第一代有区别的地方。

1
2
3
4
5
6
7
8
9
10
import json
from dataclasses import dataclass
from typing import Iterable, NamedTuple, TypeAlias, cast

import torch
import torch.nn.functional as F
from einops import rearrange, repeat
from torch import LongTensor, Tensor, nn

Device: TypeAlias = str | torch.device | None

ModelArgs 类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
@dataclass
class Mamba2Config:
    d_model: int
    n_layer: int = 24
    d_state: int = 128
    d_conv: int = 4
    expand: int = 2
    headdim: int = 64  # 多头SSM的 head dimension (P)
    chunk_size: int = 64  # 矩阵分块的尺寸 matrix partition size (Q)

	# lm 分词需要
    vocab_size: int = 50277
    pad_vocab_size_multiple: int = 16

    def __post_init__(self):
	    # 验证输入参数的正确性
        self.d_inner = self.expand * self.d_model
        assert self.d_inner % self.headdim == 0
        self.nheads = self.d_inner // self.headdim
        
        if self.vocab_size % self.pad_vocab_size_multiple != 0:
            self.vocab_size += (
                self.pad_vocab_size_multiple
                - self.vocab_size % self.pad_vocab_size_multiple
            )

Mamba2 类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
class Mamba2(nn.Module):
    def __init__(self, args: Mamba2Config, device: Device = None):
        super().__init__()
        self.args = args
        self.device = device

		# 一次性投影出所有依赖输入的参数，顺序如下
        # Order: (z, x, B, C, dt)
        d_in_proj = 2 * args.d_inner + 2 * args.d_state + args.nheads
        self.in_proj = nn.Linear(args.d_model, d_in_proj, bias=False, device=device)

        conv_dim = args.d_inner + 2 * args.d_state
        self.conv1d = nn.Conv1d(
            in_channels=conv_dim,
            out_channels=conv_dim,
            kernel_size=args.d_conv,
            groups=conv_dim,
            padding=args.d_conv - 1,
            device=device,
        )

        self.dt_bias = nn.Parameter(torch.empty(args.nheads, device=device))
        self.A_log = nn.Parameter(torch.empty(args.nheads, device=device))
        self.D = nn.Parameter(torch.empty(args.nheads, device=device))
        self.norm = RMSNorm(args.d_inner, device=device)
        self.out_proj = nn.Linear(args.d_inner, args.d_model, bias=False, device=device)

    def forward(self, u: Tensor, h: InferenceCache | None = None):
        """
        Arguments
            u: (batch, seqlen, d_model) input. seqlen should be a multiple of chunk_size.
            h: hidden states for inference step. Initialized to 0s if not present.

        Return (y, h)
            y: (batch, seqlen, d_model) output
            h: updated inference cache after processing `u`
        """
        if h:
            return self.step(u, h)

        A = -torch.exp(self.A_log)  # (nheads,)
        zxbcdt = self.in_proj(u)  # (batch, seqlen, d_in_proj)
        z, xBC, dt = torch.split(
            zxbcdt,
            [
                self.args.d_inner,
                self.args.d_inner + 2 * self.args.d_state,
                self.args.nheads,
            ],
            dim=-1,
        )
        dt = F.softplus(dt + self.dt_bias)  # (batch, seqlen, nheads)

		# 将 x, B, C 调整形状和截断，一次性进行 conv1d 后再分离开
        # Pad or truncate xBC seqlen to d_conv
        conv_state = F.pad(
            rearrange(xBC, "b l d -> b d l"), (self.args.d_conv - u.shape[1], 0)
        )

        xBC = silu(
            self.conv1d(xBC.transpose(1, 2)).transpose(1, 2)[:, : u.shape[1], :]
        )  # (batch, seqlen, d_inner + 2 * d_state))
        x, B, C = torch.split(
            xBC, [self.args.d_inner, self.args.d_state, self.args.d_state], dim=-1
        )

		# 将x分为p个部分做多头SSD
        x = rearrange(x, "b l (h p) -> b l h p", p=self.args.headdim)
        y, ssm_state = ssd(
            x * dt.unsqueeze(-1),
            A * dt,
            rearrange(B, "b l n -> b l 1 n"),
            rearrange(C, "b l n -> b l 1 n"),
            self.args.chunk_size,
            device=self.device,
        )
        y = y + x * self.D.unsqueeze(-1)
        y = rearrange(y, "b l h p -> b l (h p)")
        y = self.norm(y, z)
        y = self.out_proj(y)

        h = InferenceCache(conv_state, ssm_state)
        return y, h

    def step(self, u: Tensor, h: InferenceCache) -> tuple[Tensor, InferenceCache]:
        """Take a single inference step for the current input and hidden state

        Arguments
            u: (batch, 1, d_model)
            h: initial/running hidden state

        Return (y, h)
            y: (batch, 1, d_model)
            h: updated hidden state
        """
        assert u.shape[1] == 1, "Only one token can be decoded per inference step"

        zxbcdt = self.in_proj(u.squeeze(1))  # (batch, d_in_proj)
        z, xBC, dt = torch.split(
            zxbcdt,
            [
                self.args.d_inner,
                self.args.d_inner + 2 * self.args.d_state,
                self.args.nheads,
            ],
            dim=-1,
        )

        # Advance convolution input
        h.conv_state.copy_(torch.roll(h.conv_state, shifts=-1, dims=-1))
        h.conv_state[:, :, -1] = xBC
        # Convolution step
        xBC = torch.sum(
            h.conv_state * rearrange(self.conv1d.weight, "d 1 w -> d w"), dim=-1
        )
        xBC += self.conv1d.bias
        xBC = silu(xBC)

        x, B, C = torch.split(
            xBC, [self.args.d_inner, self.args.d_state, self.args.d_state], dim=-1
        )
        A = -torch.exp(self.A_log)  # (nheads,)

        # SSM step
        dt = F.softplus(dt + self.dt_bias)  # (batch, nheads)
        dA = torch.exp(dt * A)  # (batch, nheads)
        x = rearrange(x, "b (h p) -> b h p", p=self.args.headdim)
        dBx = torch.einsum("bh, bn, bhp -> bhpn", dt, B, x)
        h.ssm_state.copy_(h.ssm_state * rearrange(dA, "b h -> b h 1 1") + dBx)
        y = torch.einsum("bhpn, bn -> bhp", h.ssm_state, C)
        y = y + rearrange(self.D, "h -> h 1") * x
        y = rearrange(y, "b h p -> b (h p)")
        y = self.norm(y, z)
        y = self.out_proj(y)

        return y.unsqueeze(1), h

Mamba2LMHeadModel 类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
class Mamba2LMHeadModel(nn.Module):
    def __init__(self, args: Mamba2Config, device: Device = None):
        super().__init__()
        self.args = args
        self.device = device

        self.backbone = nn.ModuleDict(
            dict(
	            # 语言模型的词嵌入相关
                embedding=nn.Embedding(args.vocab_size, args.d_model, device=device),
                # 多层 SSD
                layers=nn.ModuleList(
                    [
                        nn.ModuleDict(
                            dict(
                                mixer=Mamba2(args, device=device),
                                norm=RMSNorm(args.d_model, device=device),
                            )
                        )
                        for _ in range(args.n_layer)
                    ]
                ),
                norm_f=RMSNorm(args.d_model, device=device),
            )
        )
        self.lm_head = nn.Linear(
            args.d_model, args.vocab_size, bias=False, device=device
        )
        self.lm_head.weight = self.backbone.embedding.weight

    @staticmethod
    def from_pretrained(huggingface_model_id: str, device: Device = None):
        from transformers.utils import CONFIG_NAME, WEIGHTS_NAME
        from transformers.utils.hub import cached_file

        config_path = cached_file(huggingface_model_id, CONFIG_NAME)
        assert config_path, "Failed to get huggingface config file"
        state_dict_path = cached_file(huggingface_model_id, WEIGHTS_NAME)
        assert state_dict_path, "Failed to get huggingface state dict file"

        config = json.load(open(config_path))
        args = Mamba2Config(
            d_model=config["d_model"],
            n_layer=config["n_layer"],
            vocab_size=config["vocab_size"],
            pad_vocab_size_multiple=config["pad_vocab_size_multiple"],
        )

        map_location = "cpu" if device is None else device
        state_dict = torch.load(
            state_dict_path, weights_only=True, map_location=map_location, mmap=True
        )
        model = Mamba2LMHeadModel(args, device=device)
        model.load_state_dict(state_dict)
        model.eval()
        return model

    def forward(
        self, input_ids: LongTensor, h: list[InferenceCache] | list[None] | None = None
    ) -> tuple[LongTensor, list[InferenceCache]]:
        """
        Arguments
            input_ids: (batch, seqlen) tokens from `EleutherAI/gpt-neox-20b` tokenizer
            h: hidden states for inference step. If present the constant-time
               (wrt sequence length) inference path will be taken, input_ids
               should have shape (batch, 1) containing the next batch of prompt
               token.

        Return (logits, h)
            logits: (batch, seqlen, vocab_size)
            h: updated inference cache after processing `input_ids`
        """
        seqlen = input_ids.shape[1]

        if h is None:
            h = [None for _ in range(self.args.n_layer)]

        x = self.backbone.embedding(input_ids)
        for i, layer in enumerate(self.backbone.layers):
            y, h[i] = layer.mixer(layer.norm(x), h[i])
            x = y + x

        x = self.backbone.norm_f(x)
        logits = self.lm_head(x)
        return logits[:, :seqlen], cast(list[InferenceCache], h)

    def generate(
        self,
        input_ids: LongTensor,
        max_new_length: int = 20,
        temperature: float = 1.0,
        top_k: int = 50,
        top_p: float = 1.0,
        eos_token_id: int = 0,
    ) -> Iterable[tuple[int, list[InferenceCache]]]:
        prefix, tokens = input_ids[:-1], input_ids[-1:].unsqueeze(0)

        # Process prompt
        # The input sequence to forward (non-inference path) must have length multiple that of chunk_size.
        # We split out excess tokens so that n_chunked tokens can be processed by one forward call and
        # process the rest in multiple inference steps.
        n_chunked = (prefix.shape[0] // self.args.chunk_size) * self.args.chunk_size
        if n_chunked > 0:
            _, h = self(prefix[:n_chunked].unsqueeze(0), None)
        else:
            h = [
                InferenceCache.alloc(1, self.args, device=self.device)
                for _ in range(self.args.n_layer)
            ]
        for i in range(n_chunked, prefix.shape[0]):
            _, h = self(prefix[i : i + 1].unsqueeze(0), h)

        # Generate
        for _ in range(max_new_length):
            with torch.no_grad():
                out, h = self(tokens, h)
            logits = out[0, -1]
            if temperature != 1.0:
                logits = logits / temperature
            if top_k > 0:
                indices_to_remove = logits < torch.topk(logits, k=top_k)[0][-1]
                logits[indices_to_remove] = -torch.inf
            if top_p < 1.0:
                sorted_logits, sorted_indices = torch.sort(logits, descending=True)
                cum_probs = torch.cumsum(F.softmax(sorted_logits, dim=-1), dim=-1)
                sorted_indices_to_remove = cum_probs > 0.5
                sorted_indices_to_remove[1:] = sorted_indices_to_remove[:-1].clone()
                sorted_indices_to_remove[0] = False
                indices_to_remove = sorted_indices[sorted_indices_to_remove]
                logits[indices_to_remove] = -torch.inf
            probs = F.softmax(logits, dim=-1)
            next_token = torch.multinomial(probs, num_samples=1)
            if next_token.item() == eos_token_id:
                return
            tokens = next_token.unsqueeze(0)
            yield cast(int, next_token.item()), h

ssd() 函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
def ssd(x, A, B, C, chunk_size, initial_states=None, device: Device = None):
    """Structed State Space Duality (SSD) - the core of Mamba-2

    This is almost the exact same minimal SSD code from the blog post.

    Arguments
        x: (batch, seqlen, n_heads, d_head)
        A: (batch, seqlen, n_heads)
        B: (batch, seqlen, n_heads, d_state)
        C: (batch, seqlen, n_heads, d_state)

    Return
        y: (batch, seqlen, n_heads, d_head)
    """
    assert x.shape[1] % chunk_size == 0

    # Rearrange into chunks
    # Step 1, 2 and 4 of SSD can be computed in parallel for each chunk across devices (sequence parallel)
    # This is not implemented and left as an exercise for the reader 😜
    x, A, B, C = [
        rearrange(m, "b (c l) ... -> b c l ...", l=chunk_size) for m in (x, A, B, C)
    ]

    A = rearrange(A, "b c l h -> b h c l")
    A_cumsum = torch.cumsum(A, dim=-1)

    # 1. Compute the output for each intra-chunk (diagonal blocks)
    L = torch.exp(segsum(A, device=device))
    Y_diag = torch.einsum("bclhn, bcshn, bhcls, bcshp -> bclhp", C, B, L, x)

    # 2. Compute the state for each intra-chunk
    # (right term of low-rank factorization of off-diagonal blocks; B terms)
    decay_states = torch.exp(A_cumsum[:, :, :, -1:] - A_cumsum)
    states = torch.einsum("bclhn, bhcl, bclhp -> bchpn", B, decay_states, x)

    # 3. Compute the inter-chunk SSM recurrence; produces correct SSM states at chunk boundaries
    # (middle term of factorization of off-diag blocks; A terms)
    if initial_states is None:
        initial_states = torch.zeros_like(states[:, :1])
    states = torch.cat([initial_states, states], dim=1)
    decay_chunk = torch.exp(segsum(F.pad(A_cumsum[:, :, :, -1], (1, 0)), device=device))
    new_states = torch.einsum("bhzc, bchpn -> bzhpn", decay_chunk, states)
    states, final_state = new_states[:, :-1], new_states[:, -1]

    # 4. Compute state -> output conversion per chunk
    # (left term of low-rank factorization of off-diagonal blocks; C terms)
    state_decay_out = torch.exp(A_cumsum)
    Y_off = torch.einsum("bclhn, bchpn, bhcl -> bclhp", C, states, state_decay_out)

    # Add output of intra-chunk and inter-chunk terms (diagonal and off-diagonal blocks)
    Y = rearrange(Y_diag + Y_off, "b c l h p -> b (c l) h p")

    return Y, final_state

参考

  1. A Visual Guide to Mamba and State Space Models - Maarten Grootendorst
  2. 一文通透想颠覆Transformer的Mamba：从SSM、HiPPO、S4到Mamba_mamba模型-CSDN博客
  3. 通透理解FlashAttention与FlashAttention2：全面降低显存读写、加快计算速度-CSDN博客
  4. State Space Duality (Mamba-2) Part III - The Algorithm | Tri Dao
  5. 一文通透mamba2「力证Transformer are SSM」：从SSM、半可分矩阵、SMA、SSD到mamba2-CSDN博客