相关定义与分类
多任务学习(Multi-task learning, MTL)最早可以追溯到1993年的一篇文章,它描述的是一种学习范式——多个任务的数据一起来学习,学习的效果有可能要比每个任务单独学习的结果要好。本质上是利用多个任务的共享信息来提高在所有任务上的泛化性。
多任务学习可以认为是迁移学习的一种表现形式:
Wasi Ahmad的《Multi-Task Machine Learning》
参数共享形式
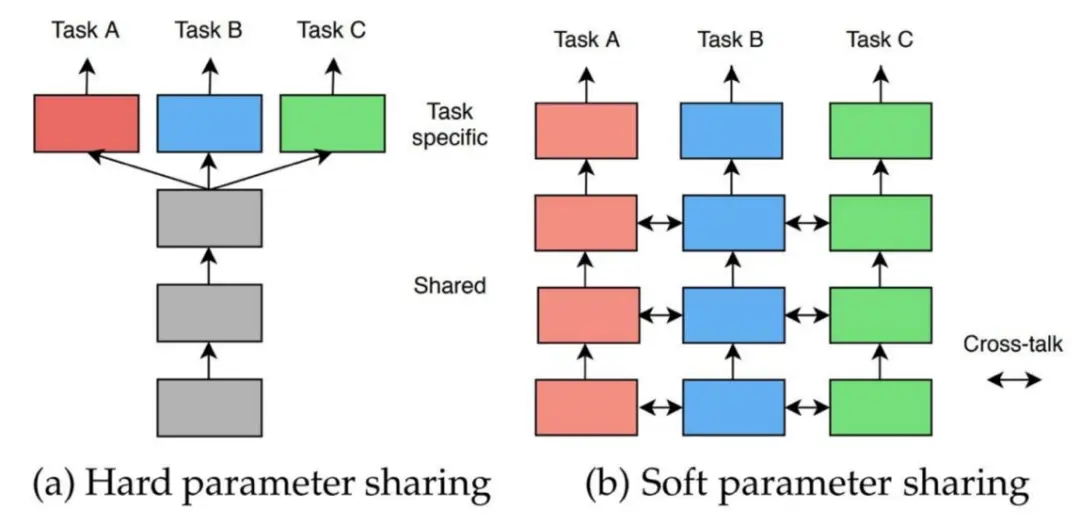
- 参数的硬共享机制:硬共享是神经网络的多任务学习中最常见的一种方式。一般来讲,它可以应用到所有任务的所有隐层上,而保留任务相关的输出层。硬共享机制降低了过拟合的风险。有文献证明了该机制过拟合风险为O(#Tasks).
- 参数的软共享机制:软共享机制下的每个任务都有自己的模型和自己的参数,但是对模型参数的距离进行了正则化来保证参数相似,例如 L2正则化,迹正则化(trace norm)等.
目标函数设计
θsh,θ1,…,θTmint=1∑TctL^t(θsh,θt)
待更
不确定性加权
不确定性加权(Uncertainty Weighting)是 Alex Kendall 等人提出的一种动态调整不同任务的权重实现多任务学习的方法。
作者引入了贝叶斯学派的思想,假设每一个子任务的预测结果对真值的后验概率服从于正态分布:
p(y∣fW(x))=N(fW(x),σ2)
其中σ 为观测噪声,将其作为标准差时,其大小代表了模型拟合效果的难易程度。
直观理解就是预测值总是在真值附近波动.
接下来考虑多任务场景,特别地以两个回归任务为例,其联合分布就可以表示为:
p(y1,y2∣fW(x))=p(y1∣fW(x))⋅p(y2∣fW(x))=N(y1;fW(x),σ12)⋅N(y2;fW(x),σ22)
我们的目标就是最大化该联合分布的似然估计,从而得出以模型参数W 和各个子任务的方差σ2 为分布参数的估计值。这等价于最小化下面的目标函数:
L(W,σ1,σ2)=−logp(y1,y2∣fW(x))∝2σ121y1−fW(x)2+2σ221y2−fW(x)2+logσ1σ2=2σ121L1(W)+2σ221L2(W)+logσ1σ2
对于分类任务,可作如下假设:
p(y∣fW(x))=Softmax(σ21fW(x))
从而通过近似可以得到相同的目标函数。回归和分类混合的多任务同样如此。
在实践中,其实就是将噪声方差σ2 也作为模型的可学习对象,从而使得模型可以自动地调整目标函数中各个损失项的权重,然后在目标函数末尾加上正则项log(σ) 防止参数σ 过大,权重为 0。
同时具体到代码上,其实是参数化s:=logσ2 ,然后参与计算时在指数计算回去,即σ2=exp(s) . 因为这能够保证参数化时满足σ2>0 的约束,同时也保证了权重1/σ2 不会为 Nan 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
log_var_a = torch.zeros((1,), requires_grad=True)
log_var_b = torch.zeros((1,), requires_grad=True)
params = ([p for p in model.parameters()] + [log_var_a] + [log_var_b])
optimizer = optim.Adam(params)
def criterion(y_pred, y_true, log_vars):
loss = 0
for i in range(len(y_pred)):
precision = torch.exp(-log_vars[i])
diff = (y_pred[i]-y_true[i])**2.
loss += torch.sum(precision * diff + log_vars[i], -1)
return torch.mean(loss)
|
值得注意的是,因为损失项的权重1/σ2 也是模型学习得到的,所以面对那些很难拟合的子任务L(W),模型会本能地/贪心地 抑制这一项所占的比例。所以该方法反而会使模型关注那些简单的任务。如果作业时目标是希望学习到应对难任务的模型,那么该方法反而可能会降点 23333。
帕累托最优
Sener O, Koltun V. Multi-task learning as multi-objective optimization[J]. Advances in neural information processing systems, 2018, 31.
处理多任务损失的另一个方法是最优化领域的视角。一个很直观的理解就是给多个损失项乘以或静态或动态的权重,其实就是将多目标优化问题转变为了优化加权后的单目标优化问题。但这种调权重的方法的问题是,如果多个任务间存在竞争关系——一个任务变好,其它任务就会变差,那么就很难找到一组有效的权重了。
帕累托最优(Pareto optimal)是经济学中的一种资源分配的理想状态,而在多目标优化领域,就代表在刚开始优化时,每个任务都能变好,直到优化到某一步时,发现一个任务变好但至少有一个其他任务会变差,那么我们就认为达到了帕累托最优(的这样一个临界状态),优化结束。
问题转换
应用帕累托最优策略,我们需要先将MTL原来的单目标优化恢复成多目标优化:
θshθ1,…,θTminL(θsh,θ1,…,θT)=θshθ1,…,θTmin(L^1(θsh,θ1),…,L^T(θsh,θT))⊤
根据优化方向的一篇数学论文里提出的 Multiple Gradient Descent Algorithm (MGDA),我们可以通过求其 KKT 条件来寻找满足帕累托最优的驻点。
- 对于所有的任务∀t,∇θtL^t(θsh,θt)=0;
- ∃α1,…,αT≥0 s.t. ∑t=1Tαt=1 使得∑t=1Tαt∇θshL^t(θsh,θt)=0.
对于第一个条件,因为是对子任务自己的网络参数θt 求梯度,要优化满足这个条件等同于平时正常地使用梯度下降来求解。
对于第二个条件,MGDA给出了证明,如果能最小化下面的目标函数为0,那么就得出了对应的驻点;如果没法为0,该目标函数的优化同样能得出可以改善性能的解。
α1,…,αTmin⎩⎨⎧t=1∑Tαt∇θshL^t(θsh,θt)22t=1∑Tαt=1,αt≥0∀t⎭⎬⎫
该优化问题,本质上就是在一个凸包里找一个点,使其距离所有的已知点都尽可能最近。这是在优化方向被广泛研究的问题。例如 Frank-Wolfe算法就是求解这类带约束的凸优化问题的一种算法。
参数更新算法
综上所述,我们可以得到一个完整的更新网络参数的算法:

先梯度下降更新 任务自己的网络参数θt ,然后使用Frank-Wolfe算法求解得到合适的α,通过加权更新共享网络参数θsh.
链式改进
上述算法虽然可以求解问题,但效率太低。直观表现就是每个任务都要计算针对共享参数的梯度∇θtL^t(θsh,θt),从而反向传播的计算量就和任务的数量成正比;当共享参数量很大时,非常低效。
作者专门针对 encoder-decoder的网络,提出了以encoder的输出Z 为界的优化方案,将反向传播的链条分成两部分:
ft(x;θsh,θt)zi=(ft(⋅;θt)∘g(⋅;θsh))(x)=ft(g(x;θsh);θt)=g(x;θsh)
将压缩层的表征向量记为Z ,从而可以得出原优化目标的理论上界,即:
t=1∑Tαt∇θshL^t(θsh,θt)22≤∂θsh∂Z22t=1∑Tαt∇ZL^t(θsh,θt)22
这样做的好处是,反向传播时每个任务的只需要计算对Z 的梯度即可,Z 的量级相比θsh 小很多,因此计算量会大大减小。此外,上界存在与α 无关系数∂θsh∂Z22 ,使用可以去掉。
用该上界替换原优化目标,优化问题就近似成:
α1,…,αTmin⎩⎨⎧t=1∑Tαt∇ZL^t(θsh,θt)22∣t=1∑Tαt=1,αt≥0∀t⎭⎬⎫
文章证明了这种近似依然能达到帕累托最优。
参考
- 当我们在谈论Multi-Task Learning(多任务/多目标学习) - 知乎
- 机器学习技术:多任务学习综述! - 知乎
- 多任务学习概述 - Harlin’s blog
- 论文讲解~CVPR2021跨领域多任务学习 Cross-Domain Multi-task Learning for Object Detection and Saliency Estimation - 知乎





