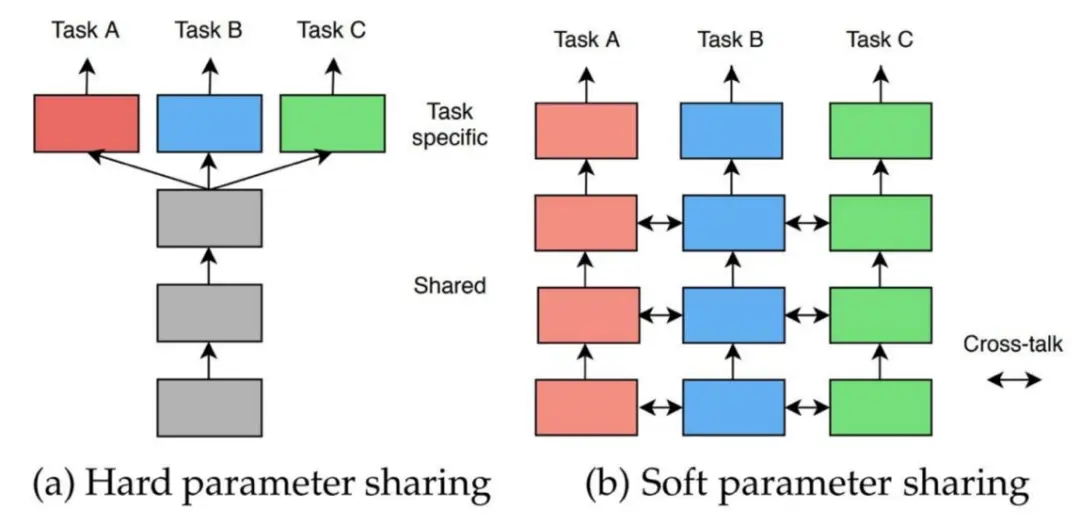
恒等映射,残差神经网络的核心思想
模型退化
随着神经网络的不断发展,越来越深的网络层在现代硬件的加持下成为了可能,并且也切实带来了更好的训练效果。深度学习的研究者们致力于增加和尝试不同的网络、构建更深的网络来尝试获得更好的结果,为了取得质的突破。
然而事与愿违,神经网络似乎并不是越深越好,人们发现当模型层数增加到某种程度,模型的效果将会不升反降。也就是说,深度模型发生了退化(degradation)。
这种退化与以往的过拟合、梯度消失或爆炸问题有着本质的不同。
有推测说,神经网络越来越深的时候,反传回来的梯度之间的相关性会越来越差,最后接近白噪声。因为我们知道图像是具备局部相关性的,那其实可以认为梯度也应该具备类似的相关性,这样更新的梯度才有意义,如果梯度接近白噪声,那梯度更新可能根本就是在做随机扰动。(The Shattered Gradients Problem: If resnets are the answer, then what is the question?)
还有一种理解,层数的增加会扩大解空间,使得结果接近最优解的可能性降低。
总而言之,各类激活函数和网络的构造给了模型足够的灵活性,而越多的网络层反而让模型“忘记了初心”。
恒等映射
按理说,当我们堆叠一个模型时,理所当然的会认为效果会越堆越好。因为,假设一个比较浅的网络已经可以达到不错的效果,那么即使之后堆上去的网络什么也不做,模型的效果也不会变差。
然而事实上,这却是问题所在。“ 什么都不做 ”恰好是当前神经网络最难做到的东西之一。
对应模型这种偏离最优映射的情况,可以用函数族来形式化地说明。
函数族
假设有⼀类特定的神经⽹络架构,它包括学习速率和其他超参数设置。
对于任意,它总能通过在合适的数据集上进⾏训练⽽确定出合适的参数集,特定的参数集就能将 具体到。
若 是我们真正想要找到的函数(在数据集上表现是最好的),那么
当 时,那我们可以直接通过训练 得到它,但通常我们不会那么幸运。
相反,我们训练只会得到⼀个函数,这是我们在 中索尼得到的最佳选择,即:
那么,怎样得到更近似 的函数呢?唯⼀合理的可能性是,我们需要设计⼀个更强⼤的架构 。
接下来的理论将告诉我们,如果,则⽆法保证新的体系“更近似”,甚至更遭。
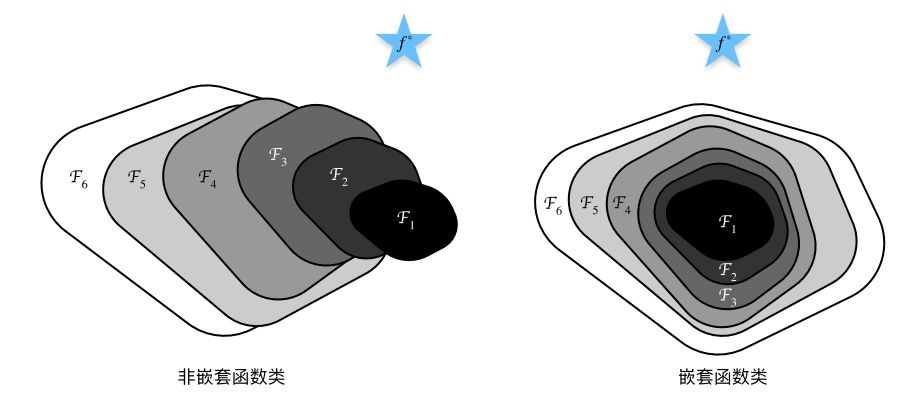
如图所⽰,对于⾮嵌套函数(non-nested function)族,较复杂的函数类并不总是向“真”函数靠拢(复杂度由 向 递增)。相反对于右侧的嵌套函数(nested function)族:,可以在复杂度增加的同时,在不偏离原来的解空间的情况下,慢慢接近目标函数。
不断加深网络层,因为激活函数的非线性等问题,就相当于得到了一系列非嵌套函数族的网络框架。而我们的目标就是想办法得到完全包含浅层网络的深层网络,形成嵌套函数族。
残差神经网络
残差设计
针对这上述问题,何恺明等⼈提出了残差⽹络(ResNet)。它在2015年的ImageNet图像识别挑战赛夺魁,并深刻影响了后来的深度神经⽹络的设计。
ResNet的核心思想就是,在浅层网络的基础上,保证新增加的网络层只学习恒等映射。(identity function)
即保证第 层网络的输出,其中 是第 层的输出。
如果实现了这样的恒等映射,那么无论添加多少层我都能保证深层网络的结果与浅层网络的结果一致!
虽然这看似用处不大,但实际上因为神经网络的灵活性,模型输出会在此基础上发散,也就是符合了前面提到的嵌套函数族结构。
而让一个神经网络层学习恒等映射是很困难的,不过! 学习残差却容易得多!
我们让第 层的网络层学习,最后再在此基础上加上 本身,最后通过激活函数得到,即:
忽略激活函数的话,根据递推关系就有:
其中, 是浅层网络的输出,也就是没有残差结构的最后一个网络。
利用链式法则得出:
可见,有着括号中 的存在,使得残差网络的梯度不容易消失,并且模型容易学习。
于是乎,这样通过 shortcut connection 进行跨层数据通路的神经网络被设计了出来:
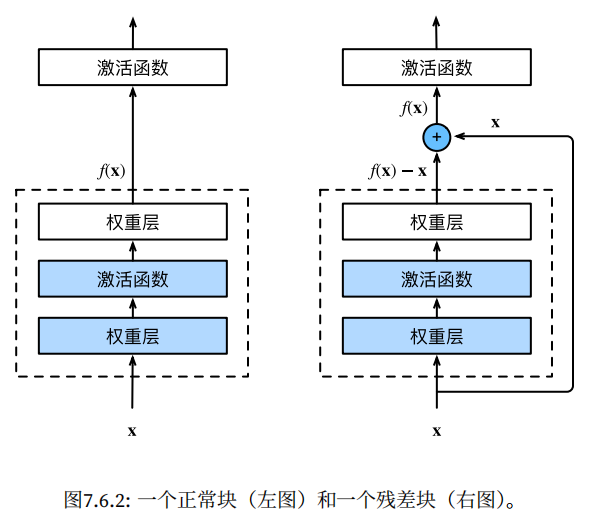
残差块和总体结构
ResNet沿⽤了VGG完整的3 × 3卷积层设计。
残差块⾥⾸先有2个有相同输出通道数的3 × 3卷积层。每个卷积层后接⼀个BN层和ReLU激活函数。
然后通过跨层数据通路,跳过这2个卷积运算,将输⼊直接加在最后的ReLU激活函数前。这样的设计要求2个卷积层的输出与输⼊形状⼀致,从⽽使它们可以相加。
如果想改变通道数,就需要引⼊⼀个额外的1 × 1卷积层来将输⼊变换成需要的形状后再做相加运算。
ResNet整体的网络结构如下图所示,足见它比此前足够深的 VGG-19 还要深。
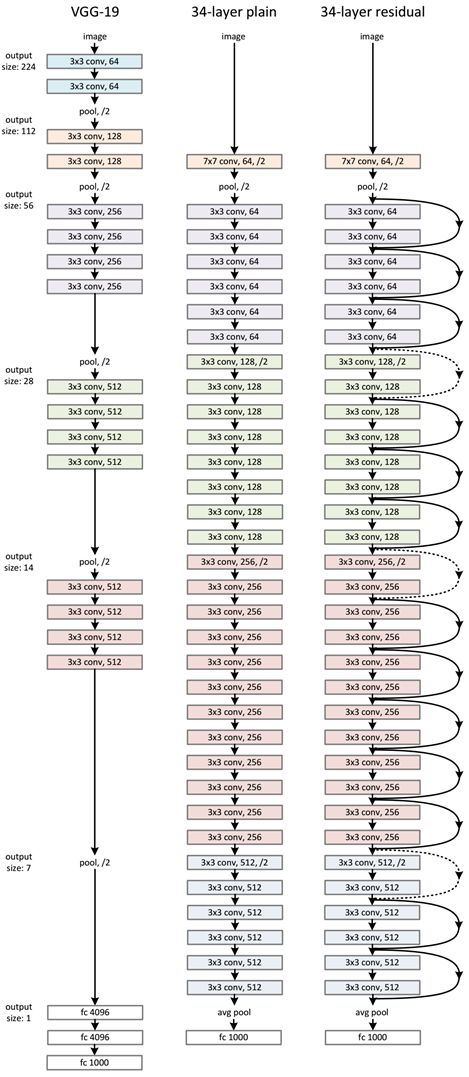
PyTorch实现
待更
稠密连接网络
吸收了 ResNet 的优点,稠密连接网络(DenseNet) 在保证网络中层与层之间最大程度的信息传输的前提下,直接将所有层连接起来。为了能够保证前馈的特性,每一层将之前所有层的输入进行拼接,之后将输出的特征图传递给之后的所有层。
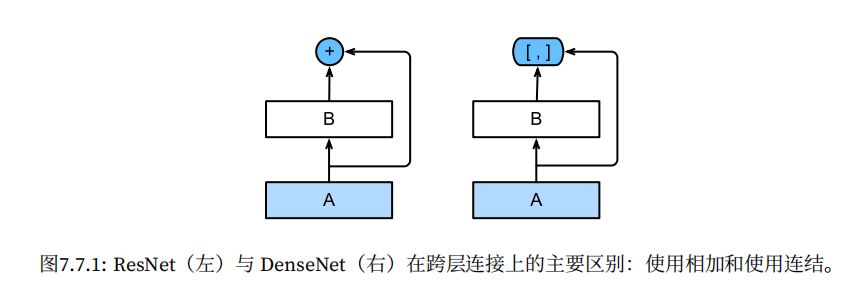
DenseNet这个名字由变量之间的“稠密连接”⽽得来,最后⼀层与之前的所有层紧密相连。
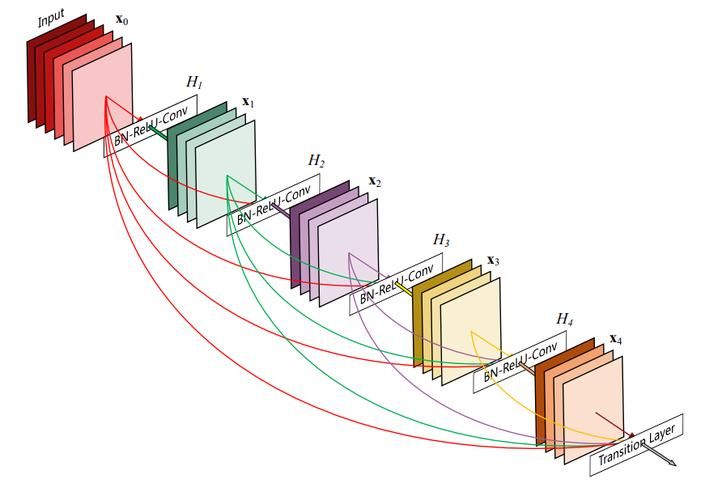
这样做有几个好处:缓解梯度消失问题、强化feature传递、鼓励feature再利用、极大减少参数总数量(这一点违反直觉,但实际上DenseNet的设计可以避免重复学习feature map;并且网络每一层的通道数非常少)。
此外,整个稠密连接⽹络主要由2部分构成:稠密块(dense block)和过渡层(transition layer)。前者定义如何连接输⼊和输出,⽽后者则通过 1×1 卷积层来控制通道数量,用池化层来减半高和宽,使其不会太复杂。