图的基本概念

本文中图的概念这一节大部分内容取自《离散数学》、图论基础-OI-Wiki

图（Graph）是图论的主要研究对象，通常由有序对 $G=(V(G),E(G),\phi)$ 表示。

$V(G)$ 表示图 $G$ 的顶点集，顶点 (vertices / nodes / points) 的集合。
$E(G)$ 表示图 $G$ 的边集，即边 (edges / links / lines / arc) 的集合。
$E$ 的元素是两个顶点构成的对 $(x,y)$ ，其中 $x$ 和 $y$ 分别表示边连接的两个端点。有： $E⊆\{(x,y)|x,y∈V\}$
$\phi$ 表示从边集到顶点对的映射，即每一条边和两个端点的对应关系。
有： $\phi:E→\{(x,y)|x,y∈V\}$

此外，我们用 $|V|$ 表示点集 $V$ 中元素的个数，也即图中的顶点个数，也被称为图的阶（Order）；同理 $|E|$ 为图的边数。

通常在讨论图时，映射关系 $\phi$ 属于默认条件，在书写时可省去，此外，在不会引起混淆的情况下， $V(G),E(G)$ 也可以简写为 $V,G$ ，即一个图可以直接写为 $G=(V,E)$ .

注：线性表可以是空表，树可以是空树，但图不可以是空图。
也就是说，图中不能一个顶点也没有，图的顶点集 $V$ 一定非空，但边集 $E$ 可以为空，此时图中只有顶点而没有边，这种图也叫零图。

有向图与无向图

无向图 (Undirected graph) 是边集 $E$ 中的元素是无序顶点对时的图，一个无序顶点对可记为 $(u,v)$ 或 $(v,u)$ ，二者等价.

有向图 (Directed graph) 是边集 $E$ 中的元素是有序顶点对时的图，也即边是有向边（也称：弧）的图。一个弧/有序对可记为： $<u,v>$ ，称：从 $u$ 到 $v$ 的弧，不可交换次序。

下图是一个有向图和无向图的简单示例：

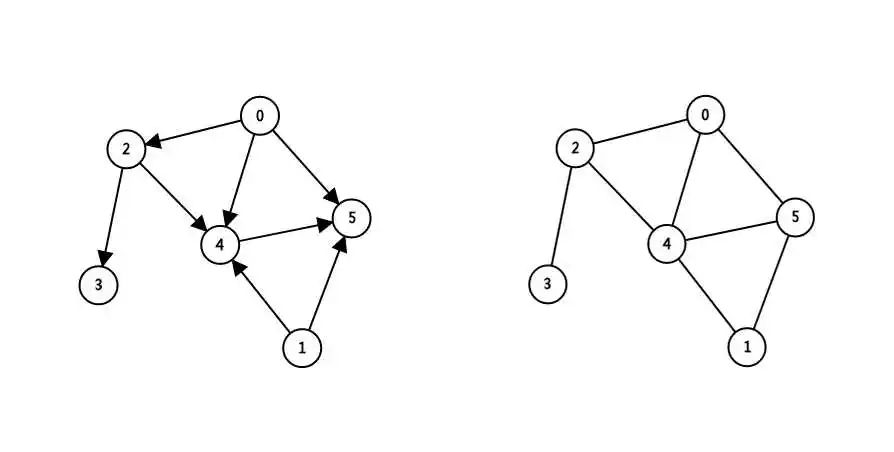
有向图和无向图

对于上图，有：

$\begin{aligned} G_1&=(V,E_1),\;G_2=(V,E_2)\\\\ \text{where }\;V&=\{0,1,2,3,4,5\}\\ E_1&=\{(0,2),(0,4),(0,5),(1,4),(1,5),(2,3),(2,4),(4,5)\}\\ E_2&=\{<0,2>,<0,4>,<0,5>,<1,4>,<1,5>,<2,3>,<2,4>,<4,5>\} \end{aligned}$

有时，为了直观和简便，我们也直接把 $G(V,E)$ 作为无向图的表示， $G<V,E>$ 作为有向图的表示。

🦄此外，还有：

若 $G$ 为混合图 (mixed graph)，则 $G$ 中既有向边，又有无向边。
若 $G$ 的每条边 $e_k=(u_k,v_k)$ 都被赋予一个数作为该边的权，则称 $G$ 为 赋权图/带权图，也称网。如果这些权都是正实数，就称 $G$ 为 正权图。

相邻与度数

在无向图 $G = (V, E)$ 中，若点 $v$ 是边 $e$ 的一个端点，则称 $v$ 和 $e$ 是 关联的 (incident) 或 相邻的 (adjacent)。对于两顶点 $u$ 和 $v$ ，若存在边 $(u, v)$ ，则称 $u$ 和 $v$ 是 相邻的 (adjacent)。

一个顶点 $v \in V$ 的 邻域 (neighborhood) 是所有与之相邻的顶点所构成的集合，记作 $N(v)$ 。

一个点集 $S$ 的邻域是所有与 $S$ 中至少一个点相邻的点所构成的集合，记作 $N(S)$ ，即：

$N(S) = \bigcup_{v \in S} N(v)$

以我们上面给出的无向图 $G_2$ 为例，
对于其中的一个顶点 $v=4$ ，有 $N(v)=\{0,1,2,5\}$ ，即与顶点 $4$ 相邻的点有 $0,1,2,5$ 。
对于其中两个点组成的点集 $S=\{2,3\}$ ，则 $N(S)=N(2)\cup N(3)=\{0,2,4\}$ 。

与一个顶点 $v$ 关联的边的条数称作该顶点的 度 (degree)，记作 $d(v)$ 。特别地，对于边 $(v, v)$ ，则每条这样的边要对 $d(v)$ 产生 $2$ 的贡献。

对于无向简单图，有 $d(v) = \left| N(v) \right|$ 。

握手定理（又称图论基本定理）：对于任何无向图 $G = (V, E)$ ，有 $\sum\limits_{v \in V} d(v) = 2 \left| E \right|$ 。

推论：在任意图中，度数为奇数的点必然有偶数个。

此外，

若 $d(v) = 0$ ，则称 $v$ 为 孤立点 (isolated vertex)。
若 $d(v) = 1$ ，则称 $v$ 为 叶结点 (leaf vertex)/悬挂点 (pendant vertex)。
若 $2 \mid d(v)$ ，则称 $v$ 为 偶点 (even vertex)。
若 $2 \nmid d(v)$ ，则称 $v$ 为 奇点 (odd vertex)。图中奇点的个数是偶数。
若 $d(v) = \left| V \right| - 1$ ，则称 $v$ 为 支配点 (universal vertex)。

对一张图，所有点的度数的最小值称为 $G$ 的 最小度 (minimum degree)，记作 $\delta (G)$ ；最大值称为 最大度 (maximum degree)，记作 $\Delta (G)$ 。即： $\delta (G) = \min\limits_{v \in G} d(v)$ ， $\Delta (G) = \max\limits_{v \in G} d(v)$ 。

若对一张无向图 $G = (V, E)$ ，每个顶点的度数都是一个固定的常数 $k$ ，则称 $G$ 为 $k$ - 正则图 ( $k$ -regular graph)。

同样以我们上面给出的无向图 $G_2$ 为例，
对于其中的一个顶点 $v=4$ ，有 $d(v)=|N(v)|=\#\{0,1,2,5\}=4$ ，即与顶点 $v=4$ 相邻的点的个数有 4 个，也就是说 $v=4$ 的度数为 4。因为度数 4 是偶数，所以顶点 $v=4$ 是偶点。
此外我们对每个顶点逐一求度可知，顶点4的度数最大，顶点3的度数最小。
从而有： $\delta(G_2)=1,\Delta(G_2)=4$

在有向图 $G = (V, E)$ 中，以一个顶点 $v$ 为起点的边的条数称为该顶点的 出度 (out-degree)，记作 $d^+(v)$ 。以一个顶点 $v$ 为终点的边的条数称为该节点的 入度 (in-degree)，记作 $d^-(v)$ 。显然 $d^+(v)+d^-(v)=d(v)$ 。

对于任何有向图 $G = (V, E)$ ，有：

$\sum_{v \in V} d^+(v) = \sum_{v \in V} d^-(v) = \left| E \right|$

以我们上面给出的有向图 $G_1$ 为例，
对于其中的一个顶点 $v=0$ ，有 $d^+(v)=3$ ，即以顶点 $v=0$ 为起点向与之相邻的点”射出“的弧的个数是 3。

简单图与完全图

自环 (loop/self-loop)：对 $E$ 中的边 $e = (u, v)$ ，若 $u = v$ ，则 $e$ 被称作一个自环。

重边 (multiple edge/paraller edge)：若 $E$ 中存在两个完全相同的元素（边） $e_1, e_2$ ，则它们被称作（一组）重边。

简单图 (simple graph)：若一个图中没有自环和重边，它被称为简单图。具有至少两个顶点的简单无向图中一定存在度相同的结点。

如果一张图中有自环或重边，则称它为 多重图 (multigraph)。

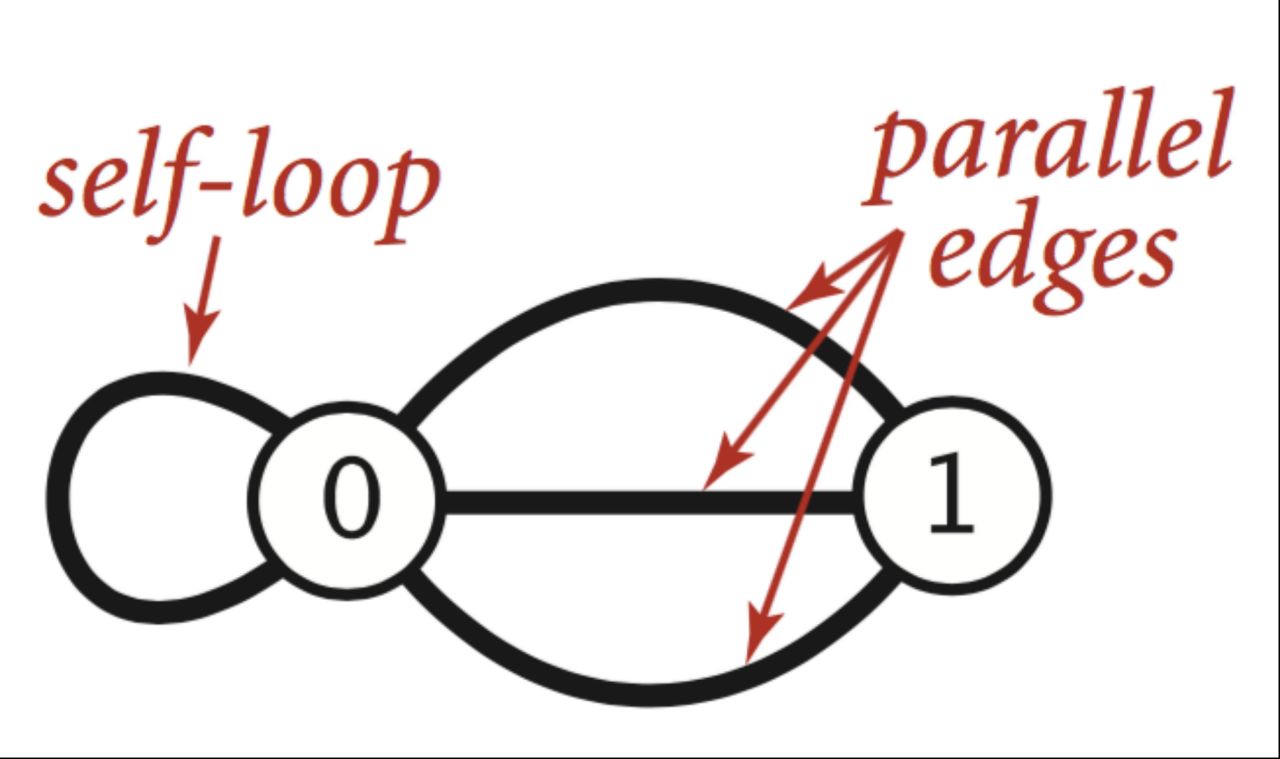
在无向图中 $(u, v)$ 和 $(v, u)$ 算一组重边，而在有向图中， $<u,v>$ 和 $<v,u>$ 不为重边。

在题目中，如果没有特殊说明，是可以存在自环和重边的，在做题时需特殊考虑。

对于任意一张简单无向图 $G = (V, E)$ ，其边数 $|E|\in[0,n(n-1)/2]$ 。当边数取最大值时，每一个顶点 $v$ 到其他顶点都有边。

若简单无向图 $G$ 满足任意不同两点间均有边，也就是边数 $|E|=n(n-1)/2=C_m^2$ 时，则称 $G$ 为 完全图 (complete graph)， $n$ 阶完全图记作 $K_n$ 。

此外，若有向图 $G$ 满足任意不同两点间都有两条方向不同的边，则称 $G$ 为 有向完全图 (complete digraph)。

示例如下：

无向完全图	有向完全图

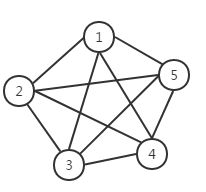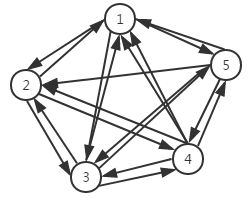边集为空的图称为 无边图 (edgeless graph)、空图 (empty graph) 或 零图 (null graph)， $n$ 阶无边图记作 $\overline{K}_n$ 或 $N_n$ 。 $N_n$ 与 $K_n$ 互为补图。

补图与反图

对于简单无向图 $G = (V, E)$ ，它的 补图 (complement graph) 记作 $\bar G$ ，满足 $V \left( \bar G \right) = V \left( G \right)$ ，且对任意结点对 $(u, v)$ ， $(u, v) \in E \left( \bar G \right)$ 当且仅当 $(u, v) \notin E \left( G \right)$ 。

事实上， $G\cup\bar{G}=\left(V,E\left(\bar{G}\right)\cup E(G)\right)$ 就是一个完全图。一个简单无向图的补图就是用其完全图减去其本身得到的图。

对于有向图 $G = (V, E)$ ，它的 反图 (transpose graph) 指的是点集不变，每条边反向得到的图，即：若 $G$ 的反图为 $G'=(V, E')$ ，则 $E'=\{(v, u)|(u, v)\in E\}$ 。

路径与连通

途径、路径和环

途径 (walk)：途径是连接一连串顶点的边的序列，可以为有限或无限长度。
形式化地说，一条有限途径 $w$ 是一个边的序列 $e_1, e_2, \ldots, e_k$ ，使得存在一个顶点序列 $v_0, v_1, \ldots, v_k$ 满足 $e_i = (v_{i-1}, v_i)$ ，其中 $i \in [1, k]$ 。这样的途径可以简写为 $v_0 \to v_1 \to v_2 \to \cdots \to v_k$ 。
通常来说，边的数量 $k$ 被称作这条途径的长度（如果边是带权的，长度通常指途径上的边权之和，题目中也可能另有定义）。

迹 (trail)：对于一条途径 $w$ ，若 $e_1, e_2, \ldots, e_k$ 两两互不相同，则称 $w$ 是一条迹。

路径 (path)（又称 简单路径 |simple path)：对于一条迹 $w$ ，若其连接的点的序列中点两两不同，则称 $w$ 是一条路径。

回路 (circuit)：对于一条迹 $w$ ，若 $v_0 = v_k$ ，则称 $w$ 是一条回路。

环/圈 (cycle)（又称 简单回路/简单环 |simple circuit)：对于一条回路 $w$ ，若 $v_0 = v_k$ 是点序列中唯一重复出现的点对，则称 $w$ 是一个环。

关于路径的定义在不同地方可能有所不同。
如，“路径”可能指本文中的“途径”，“环”可能指本文中的“回路”。如果在题目中看到类似的词汇，且没有“简单路径”/“非简单路径”（即本文中的“途径”）等特殊说明，最好询问一下具体指什么。

无向图的连通性

对于一张无向图 $G = (V, E)$ ，对于 $u, v \in V$ ，若存在一条途径能够连接 $u,v$ ，则称 $u$ 和 $v$ 是 连通的 (connected)。

由定义，任意一个顶点和自身连通，任意一条边的两个端点连通。

若无向图 $G = (V, E)$ ，满足其中任意两个顶点均连通，则称 $G$ 是 连通图 (connected graph)

$G$ 的这一性质称作 连通性 (connectivity)。

若 $H$ 是 $G$ 的一个连通子图，且不存在 $F$ 满足 $H\subsetneq F \subseteq G$ 且 $F$ 为连通图，则 $H$ 是 $G$ 的一个 连通块/连通分量 (connected component)（极大连通子图）。

换句话说， $H$ 是 $G$ 的子图中，满足 $H$ 连通且再找不到比 $H$ 的边数更大的子图。

我们有：

有回路的无向图不一定是连通图，因为其回路不一定包含所有点；
连通图可能是树也可能存在环，但一定能通过一次深度优先搜索便访问完所有结点；
连通图的生成树是它的一个极小连通子图，包含全部顶点但边数最少；
一个具有 $n$ 个顶点的无向图，若是连通图，则其边数至少有 $n$ 条，此时正好形成一个首尾相连的环；
一个具有 $n$ 个顶点的无向图，若需要保证它一定是连通图，则其边数至少需要 $(n-1)(n-2)/2+1$ 条.
其中， $n-1$ 个顶点构成完全图需要 $(n-1)(n-2)/2$ 条边，再将剩下的一个顶点与之相连，就能保证一定是连通图，所以在此基础上又消耗一条边
一个具有 $l$ 条边的无向图，若是非连通图，则其结点个数最小是多少？
本问题与第五点相对，要用更少的结点消耗更多的边，当且仅当有 $n-1$ 个结点构成完全图，剩下一个结点独立存在时。

※一定要区分第五点和第四点的区别！！！

第五点指出，若一张无向图 $G=(V,E)$ 中 $|V|=n$ ，若 $|E|\gt C_{n-1}^2$ 则该图为连通图。

有向图的连通性

对于一张有向图 $G = (V, E)$ ，对于 $u, v \in V$ ，若存在一条途径能够使得 $u\to v$ ，则称 $u$ 可达 $v$ 。

由定义，任意一个顶点可达自身，任意一条边的起点可达终点。（无向图中的连通也可以视作双向可达。）

若一张有向图的结点两两互相可达，则称这张图是 强连通的 (strongly connected)。

若一张有向图的边替换为无向边后可以得到一张连通图，则称原来这张有向图是 弱连通的 (weakly connected)。

与连通分量类似，也有 弱连通分量 (weakly connected component)（极大弱连通子图）和 强连通分量 (strongly connected component)（极大强连通子图）。

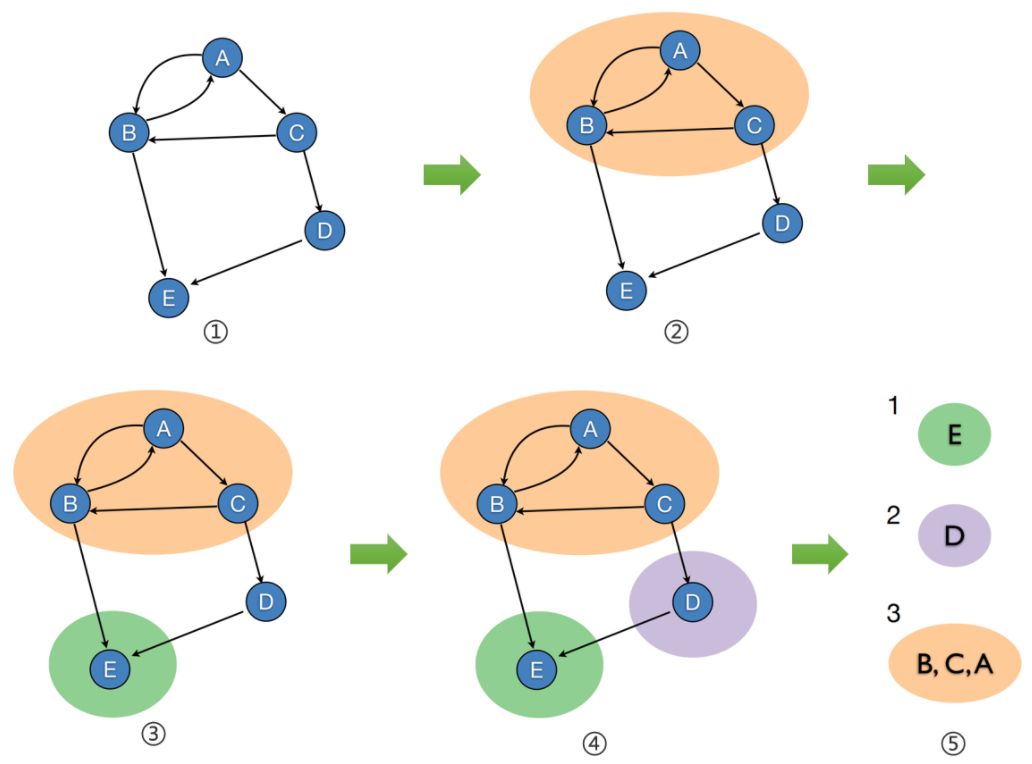
图的连通分量

上图就是一个有向图的强连通分量的划分。

子图与正则图

前面我们已经介绍了，若对一张无向图 $G = (V, E)$ ，每个顶点的度数都是一个固定的常数 $k$ ，则称 $G$ 为 $k$ - 正则图 ( $k$ -regular graph)。

下面介绍子图。

对一张图 $G = (V, E)$ ，若存在另一张图 $H = (V', E')$ 满足 $V' \subseteq V$ 且 $E' \subseteq E$ ，则称 $H$ 是 $G$ 的 子图 (subgraph)，记作 $H \subseteq G$ 。

若对 $H \subseteq G$ ，满足 $\forall u, v \in V'$ ，只要 $(u, v) \in E$ ，均有 $(u, v) \in E'$ ，则称 $H$ 是 $G$ 的 导出子图/诱导子图 (induced subgraph)。

显然，一个图的导出子图仅由子图的点集决定，因此点集为 $V'$ ( $V' \subseteq V$ ) 的导出子图称为 $V'$ 导出的子图，记作 $G \left[ V' \right]$ 。

若 $H \subseteq G$ 满足 $V' = V$ ，则称 $H$ 为 $G$ 的 生成子图/支撑子图 (spanning subgraph)。

显然， $G$ 是自身的子图，支撑子图，导出子图；无边图是 $G$ 的支撑子图。原图 $G$ 和无边图都是 $G$ 的平凡子图。

若一张无向图 $G$ 的某个生成子图 $F$ 为 $k$ -正则图，则称 $F$ 为 $G$ 的一个 $k$ -因子 ( $k$ -factor)。

如果有向图 $G = (V, E)$ 的导出子图 $H = G \left[ V^\ast \right]$ 满足 $\forall v \in V^\ast, (v, u) \in E$ ，有 $u \in V^\ast$ ，则称 $H$ 为 $G$ 的一个 闭合子图 (closed subgraph)。

割点与割边/桥

在本部分的讨论中，有向图的“连通”一般指“强连通”。

对于连通图 $G = (V, E)$ ，若 $V'\subseteq V$ 且 $G\left[V\setminus V'\right]$ （即从 $G$ 中删去 $V'$ 中的点）不是连通图，则 $V'$ 是图 $G$ 的一个 点割集 (vertex cut/separating set)。大小为一的点割集又被称作 割点 (cut vertex)。

换句话来说，对于一个连通图，如果把一个点删除后这个图的极大连通分量数增加了，那么这个点就是这个图的割点（又称割顶）。所有割点构成的集合就是点割集。

对于连通图 $G = (V, E)$ 和整数 $k$ ，若 $|V|\ge k+1$ 且 $G$ 不存在大小为 $k-1$ 的点割集，则称图 $G$ 是 $k$ - 点连通的 ( $k$ -vertex-connected)，而使得上式成立的最大的 $k$ 被称作图 $G$ 的 点连通度 (vertex connectivity)，记作 $\kappa(G)$ 。

对于非完全图，点连通度即为最小点割集的大小，而完全图 $K_n$ 的点连通度为 $n-1$ 。

对于图 $G = (V, E)$ 以及 $u, v\in V$ 满足 $u\ne v$ ， $u$ 和 $v$ 不相邻， $u$ 可达 $v$ ，若 $V'\subseteq V$ ， $u, v\notin V'$ ，且在 $G\left[V\setminus V'\right]$ 中 $u$ 和 $v$ 不连通，则 $V'$ 被称作 $u$ 到 $v$ 的点割集。 $u$ 到 $v$ 的最小点割集的大小被称作 $u$ 到 $v$ 的 局部点连通度 (local connectivity)，记作 $\kappa(u, v)$ 。

上述定义中，还可以把研究对象改成图的边：

对于连通图 $G = (V, E)$ ，若 $E'\subseteq E$ 且 $G' = (V, E\setminus E')$ （即从 $G$ 中删去 $E'$ 中的边）不是连通图，则 $E'$ 是图 $G$ 的一个 边割集 (edge cut)。大小为一的边割集又被称作 桥 (bridge)。

对于连通图 $G = (V, E)$ 和整数 $k$ ，若 $G$ 不存在大小为 $k-1$ 的边割集，则称图 $G$ 是 $k$ - 边连通的 ( $k$ -edge-connected)，而使得上式成立的最大的 $k$ 被称作图 $G$ 的 边连通度 (edge connectivity)，记作 $\lambda(G)$ 。（对于任何图，边连通度即为最小边割集的大小。）

对于图 $G = (V, E)$ 以及 $u, v\in V$ 满足 $u\ne v$ ， $u$ 可达 $v$ ，若 $E'\subseteq E$ ，且在 $G'=(V, E\setminus E')$ 中 $u$ 和 $v$ 不连通，则 $E'$ 被称作 $u$ 到 $v$ 的边割集。 $u$ 到 $v$ 的最小边割集的大小被称作 $u$ 到 $v$ 的 局部边连通度 (local edge-connectivity)，记作 $\lambda(u, v)$ 。

点双连通 (biconnected) 几乎与 $2$ - 点连通完全一致，除了一条边连接两个点构成的图，它是点双连通的，但不是 $2$ - 点连通的。换句话说，没有割点的连通图是点双连通的。

边双连通 ( $2$ -edge-connected) 与 $2$ - 边双连通完全一致。换句话说，没有桥的连通图是边双连通的。

与连通分量类似，也有 点双连通分量 (biconnected component)（极大点双连通子图）和 边双连通分量 ( $2$ -edge-connected component)（极大边双连通子图）。

🦄 Whitney 定理：对任意的图 $G$ ，有 $\kappa(G)\le \lambda(G)\le \delta(G)$ 。（不等式中的三项分别为点连通度、边连通度、最小度。）

稀疏图与稠密图

若一张图的边数远小于其点数的平方，那么它是一张 稀疏图 (sparse graph)。

若一张图的边数接近其点数的平方，那么它是一张 稠密图 (dense graph)。

一般当图 $G$ 满足 $|E|\lt |V|\log|V|$ 时，可将 $G$ 视为稀疏图。

这两个概念并没有严格的定义，一般用于讨论 时间复杂度 为 $O(|V|^2)$ 的算法与 $O(|E|)$ 的算法的效率差异：

在稠密图上这两种算法效率相当；
在稀疏图上 $O(|E|)$ 的算法效率明显更高。

其他特殊的图

若有向简单图 $G$ 满足任意不同两点间都有恰好一条边（单向），则称 $G$ 为 竞赛图 (tournament graph)。

若无向简单图 $G = \left( V, E \right)$ 的所有边恰好构成一个圈，则称 $G$ 为 环图/圈图 (cycle graph)， $n$ ( $n \geq 3$ ) 阶圈图记作 $C_n$ 。易知，一张图为圈图的充分必要条件是，它是 $2$ - 正则连通图。

若无向简单图 $G = \left( V, E \right)$ 满足，存在一个点 $v$ 为支配点，其余点之间没有边相连，则称 $G$ 为 星图/菊花图 (star graph)， $n + 1$ ( $n \geq 1$ ) 阶星图记作 $S_n$ 。

若无向简单图 $G = \left( V, E \right)$ 满足，存在一个点 $v$ 为支配点，其它点之间构成一个圈，则称 $G$ 为 轮图 (wheel graph)， $n + 1$ ( $n \geq 3$ ) 阶轮图记作 $W_n$ 。

若无向简单图 $G = \left( V, E \right)$ 的所有边恰好构成一条简单路径，则称 $G$ 为 链 (chain/path graph)， $n$ 阶的链记作 $P_n$ 。易知，一条链由一个圈图删去一条边而得。

如果一张无向连通图不含环，则称它是一棵 树 (tree)。相关内容详见树基础。

其他特殊的图

如果一张无向连通图包含恰好一个环，则称它是一棵 基环树 (pseudotree)。

如果一张有向弱连通图每个点的入度都为 $1$ ，则称它是一棵 基环外向树。

如果一张有向弱连通图每个点的出度都为 $1$ ，则称它是一棵 基环内向树。

多棵树可以组成一个 森林 (forest)，多棵基环树可以组成 基环森林 (pseudoforest)，多棵基环外向树可以组成 基环外向树森林，多棵基环内向树可以组成 基环内向森林 (functional graph)。

如果一张无向连通图的每条边最多在一个环内，则称它是一棵 仙人掌 (cactus)。多棵仙人掌可以组成沙漠。

如果一张图的点集可以被分为两部分，每一部分的内部都没有连边，那么这张图是一张 二分图 (bipartite graph)。如果二分图中任何两个不在同一部分的点之间都有连边，那么这张图是一张 完全二分图 (complete bipartite graph/biclique)，一张两部分分别有 $n$ 个点和 $m$ 个点的完全二分图记作 $K_{n, m}$ 。相关内容详见二分图。

如果一张图可以画在一个平面上，且没有两条边在非端点处相交，那么这张图是一张 平面图 (planar graph)。一张图的任何子图都不是 $K_5$ 或 $K_{3, 3}$ 是其为一张平面图的充要条件。对于简单连通平面图 $G=(V, E)$ 且 $V\ge 3$ ， $|E|\le 3|V|-6$ 。

图的存储

对于图的存储，必须保证能够准确、完整地反映顶点集和边集的信息。
不同图的结构和算法采用不同的存储方式也会对程序的效率产生较大的影响，因此所选的存储结构应该适合于待求解的问题。

直接存边法

直接使用数组来存边，数组中的每个元素都包含一条边的起点与终点（带边权的图还包含边权）。

#include <iostream> 
#include <vector> 
using namespace std; 
struct Edge {
	int u, v; 
}; // 边结构体

int n, m; // n 为顶点数, m 为边数
vector<Edge> e; 
vector<bool> vis; 

void dfs(int u) { //对图进行深度优先搜索
	if (vis[u]) return; 
	vis[u] = true; 
	for (int i = 1; i <= m; ++i) {
		if (e[i].u == u) {
			dfs(e[i].v); 
		}
	}
}

可见，采用直接存边法，其空间复杂度为 $O(|E|)$ ，遍历图的时间复杂度为 $O(|V|\times|E|)$ .

由于直接存边的遍历效率低下，一般不用于遍历图。

在 Kruskal 算法 中，由于需要将边按边权排序，需要直接存边。

在有的题目中，需要多次建图（如建一遍原图，建一遍反图），此时既可以使用多个其它数据结构来同时存储多张图，也可以将边直接存下来，需要重新建图时利用直接存下的边来建图。

邻接矩阵

使用一个二维数组 $Adj[1..n][1..n]$ 来存边，其中 $n=|V|$ 。（ Adj 其实就是邻接 Adjacent 的缩写）

我们规定：

$Adj[i][j]=\begin{cases}1,&(v_i,v_j)\in E(G)\\ 0,&(v_i,v_j)\not\in E(G) \end{cases}\quad \;,v_i,v_j\in V(G)\;\;i,j=1,2,...,n$

如果是有向图，上式将 (vi,vj) 换为有序二元组 <vi,vj> 即可。
如果是带边权的图(网)，可以在 Adj[i][j] 中存储 $v_i$ 到 $v_j$ 的边的边权 $w(v_i,v_j)$ ，此时可规定 $\infty$ 表示不存在 $v_i,v_j$ 的边。
如果是多重图，可以将 Adj[i][j] 的值定义为边的条数。

一个带权图的邻接矩阵示例如下：

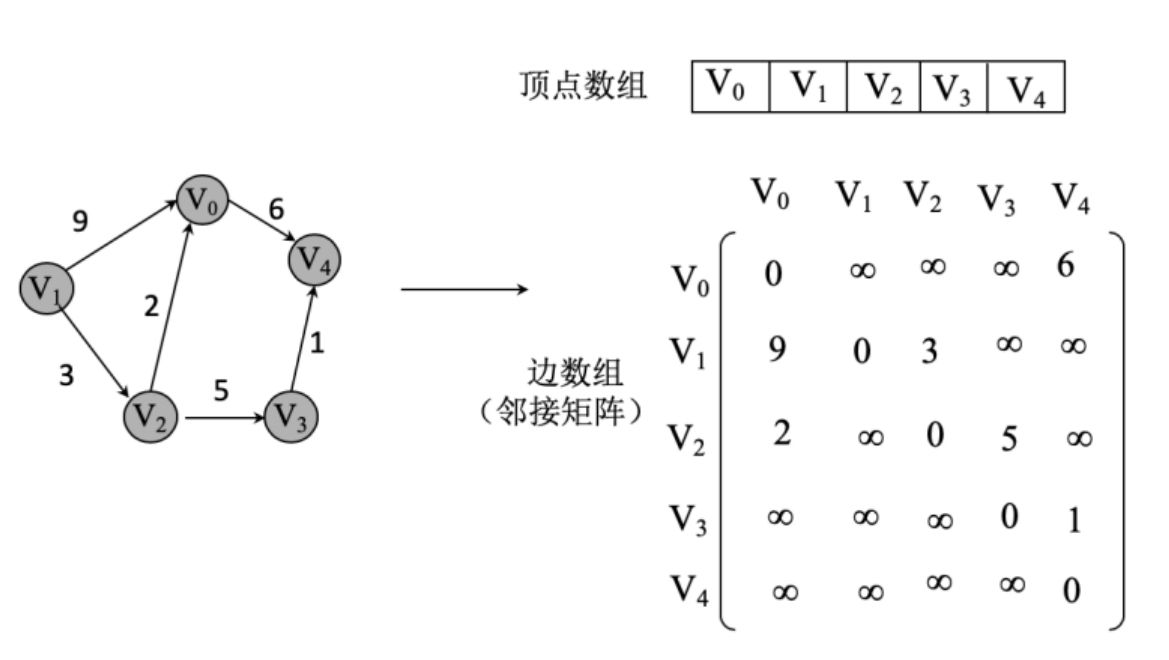
邻接矩阵示意图

不仅如此，我们还可以从邻接矩阵中直接得出如下结论：

不含自环的简单图的邻接矩阵其主对角元素均为0；
邻接矩阵存储无向图信息时，是对称矩阵；
邻接矩阵存储不带权图时，属于 0-1 矩阵；
最显著的优点是可以 $O(1)$ 查询一条边是否存在
稠密图适合使用邻接矩阵进行存储；
邻接矩阵只适用于没有重边（或重边可以忽略）的情况
邻接矩阵可以直接反映某个顶点的度或出度入度情况。如下：

$\sum_{i=1}^nAdj[i][j]=d^-(v_j),\quad\sum_{j=1}^nAdj[i][j]=d^+(v_i)$

邻接矩阵的C++ 实现如下：

#include <iostream>
#include <vector>

using namespace std;

int n, m;
vector<bool> vis;
vector<vector<bool> > adj;

bool find_edge(int u, int v) { return adj[u][v]; }

void dfs(int u) {
  if (vis[u]) return;
  vis[u] = true;
  for (int v = 1; v <= n; ++v) {
	if (adj[u][v]) {
	  dfs(v);
	}
  }
}

可见，
邻接矩阵查询是否存在某条边只需 $O(1)$ ；
遍历一个点的所有出边： $O(n)=O(|V|)$ ；
遍历整张图： $O(n^2)=O(|V|^2)$ ；
空间复杂度： $O(n^2)=O(|V|^2)$ 。

邻接矩阵的幂

二维数组 $Adj$ 对应的矩阵记为 $A$ ，则有：

$A^k$ 中的第 $(i,j)$ 个元素记为 $a_{ij}^k$ ，则它表示 $v_i$ 到 $v_j$ 中路径长度为 $m$ 的路径条数；
使得 $a_{ij}^k\gt0$ 最小的 $k$ 值，就是 $v_i$ 到 $v_j$ 的最短路径长度；
存在 $t\neq s$ 使得 $a_{ij}^t\gt0,a_{ij}^s\gt0$ ，当且仅当 $G$ 中有一条包含 $v_i,v_j$ 的回路。

记 $B_k=A+A^2+\cdots+A^k$ ，其第 $(i,j)$ 个元素记为 $b_{ij}^k$ ，则 $b_{ij}^k\gt0$ 时， $v_i$ 到 $v_j$ 存在长度不大于 $k$ 的路径。

对其作布尔运算，可以进而得出：可达性矩阵、路径矩阵等。

邻接表

邻接表是指对图 $G$ 中的每一个顶点都建立一个单链表， $\forall v_i\in V(G)$ ，它的单链表由其邻域 $N(v_i)$ 依次链入链表中得以实现，这个表就称为 $v_i$ 的边表。对于有向图，则是以 $v_i$ 为起点的弧所连接的另一个顶点依次链入得到此链表，此时称为 出边表。

边表的头指针与顶点数据信息以顺序存储，称为顶点表。
存储带权图时，还需存储边权信息。

最终得到下图所示的结构：

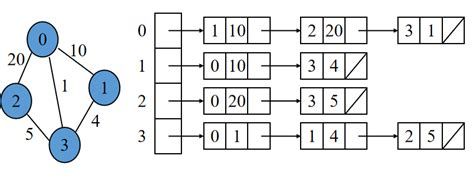
带权图的邻接表示例

邻接表存各种图都很适合，除非有特殊需求（如需要快速查询一条边是否存在，且点数较少，可以使用邻接矩阵）。
求某个顶点的出度只需计算其边表的长度即可，但求入度时则需要遍历整个表。因此，也有逆邻接表的提出，即链表采用入度表。
图的邻接表不唯一，因为边表的插入顺序可以调换。
对于稀疏图，邻接表可以极大地节省空间。

邻接表的C++ 实现如下：

//创建图的基类 Graph
class Graph{
    private:
        int a;
};

// 建立边表 包含顶点索引值、下一项指针、边权重
typedef struct ArcNode{
    int VexIndex;
    struct ArcNode *next;
    double weight; // 可忽略
}ArcNode;

// 建立顶点表 包含顶点值、边表头指针
template<class elementType>
struct VNode{
    elementType data;
    ArcNode *firstarc;
};

// 邻接表存储的图类 ALGraph
template<class elementType>
class ALGraph:public Graph{
    public:
        int VexNum;//顶点个数
        struct VNode<elementType> GraphList[MAXVEXMUN];//邻接表
        ALGraph();
        ALGraph(BinTree<elementType>* tree);
        ~ALGraph();
};

可见，
查询是否存在 $u$ 到 $v$ 的边： $O(d^+(u))$ （如果事先进行了排序就可以使用二分查找做到 $O(\log(d^+(u)))$ ）。
遍历点 $u$ 的所有出边： $O(d^+(u))$ 。
遍历整张图： $O(|E|+|V|)$ 。
空间复杂度：有向图 $O(|E|+|V|)$ ，无向图 $O(2|E|+|V|)$ ，因为每条边需要在邻接表内存储两次。

十字链表

针对有向图

邻接多重表

针对无向图

待更

图的遍历

图的遍历是指从图的某一个顶点出发，按某种搜索方法沿着图中的边对所有顶点访问且只访问一次的过程。

通过图的遍历，我们可以由此求解图的连通性问题、拓扑排序以及关键路径。

广度优先遍历

广度优先遍历又称为宽度优先搜索（Breadth First Search，BFS），是最常见的图的搜索算法之一。

广度优先遍历图的过程是指从某一顶点 $v$ 出发，一次性访问所有未被访问的邻接顶点，再依次从这些已访问过的邻接点出发，一层一层地访问。即由近至远依次访问和 $v$ 有路径相通且路径长度为 $1,2,...$ 的顶点。

算法过程可以看做是图上火苗传播的过程：
最开始只有起点着火了，在每一时刻，有火的结点都向它相邻的所有节点传播火苗。

下面给出一实例演示 BFS 的过程。
有向图和无向图

以上图为例，考虑左边的有向图，并把结点 0 作为起始点。

优先访问 0；
然后依次访问与其直接相邻的结点（以 0 作起点），即2，4，5；
访问与 2 直接相邻的 3；（与 2 相邻的 4 在上一步访问过，所以不再继续访问）
没有从 3 出发的邻接点；
与 4 相邻的 5 在上面访问过，不再继续访问；
没有从 5 出发的邻接点；
最后访问 1，结束。

最终我们得到遍历结果：024531。

考虑上图在右边的无向图，则无需讨论方向，用类似的方法可得：024531。
此外，此搜索过程可以得到一棵图的遍历树，我们称为 广度优先生成树。若是邻接矩阵存储，则生成树唯一；若是邻接表存储，则生成树不唯一。

编程实现

图的广度优先遍历的算法设计详见本站文章：经典搜索算法与分支定界技术

采用邻接表存储时，每个顶点只需搜索一次，消耗 $|V|$ 的时间，而搜索邻接点的时候每条边至少访问一次，一共消耗 $|E|$ 的时间，故时间复杂度为 $O(|E|+|V|)$ .

采用邻接矩阵存储时，每个顶点只需搜索一次，消耗 $|V|$ 的时间，而搜索每一个邻接点时都需要遍历一行或者一列，消耗 $|V|$ ，总时间复杂度为 $O(|V|^2)$ .

显然，无论是邻接表还是邻接矩阵存储， BFS 都需要辅助队列 $Q$ 的支持，在最坏情况下， $Q$ 将所有顶点都入队，则空间复杂度 $O(|V|)$ .

BFS 的图应用(部分)

♾️在一个无权图上求从起点到其他所有点的最短路径。

显然这是可行的，只需要在访问邻接点时记录其层数即可。

♾️在 $O(|E|+|V|)$ 时间内求出所有连通块。

只需要从每个没有被访问过的结点开始做 BFS，显然每次 BFS 会走完一个连通块。在前面的有向图示例中，单独的结点 1 就是一个示例。

♾️ 在一个有向无权图中找最小环。

从每个点开始 BFS，在我们即将抵达一个之前访问过的点开始的时候，就知道遇到了一个环。
注：图的最小环是每次 BFS 得到的最小环的平均值。

深度优先遍历

深度优先遍历，又称深度优先搜索**（Depth First Search），简称DFS，与 BFS 一样，它也属于一种图搜索算法。

对比来看，BFS 是按起点到邻接点的路径长度进行的遍历，而 DFS 正如其名，其过程简要来说是对每一个可能的分支路径深入到不能再深入为止地进行访问，类似于树的先序遍历。

DFS 的过程是：首先访问图的起始顶点 $v$ ，然后从 $v$ 出发，访问与之邻接的第一个结点 $w$ ，再访问与 $w$ 邻接的第一个结点 $u$ ，如此下去，直到最深处访问完毕，但仍有结点未访问时，再往上一个点回溯，然后访问其下一个邻接点（如果有）。

同样，DFS 也有对应的深度优先搜索树。若图为非连通图，则将产生深度优先搜索森林。

下面给出一实例演示 DFS 的过程。
有向图和无向图

还是以此图为例，这次我们考虑右边的无向图，并把结点 0 作为起始点。

优先访问 0；
访问与 0 直接相邻的第一个结点 2；
访问与 2 直接相邻的 3；
从 3 出发没有再往下的邻接点，于是回溯到 2 处；
访问与 2 直接相邻的除了 3 以外的下一个邻接点 4；
访问与 4 直接相邻的 1；
访问与 1 直接相邻的 5；
从 5 出发没有再往下的邻接点（其他的已经访问过了），并且已经遍历完所有结点，结束。

最终我们得到遍历结果：023415。

编程实现

图的深度优先遍历的算法设计详见本站文章：经典搜索算法与分支定界技术

显然，无论是邻接表还是邻接矩阵存储， DFS 将借助深度最大为 $|V|$ 的递归工作栈，所以空间复杂度 $O(|V|)$ .

DFS 的图应用(部分)

♾️判断一个图 $G$ 是否为一棵树

$G$ 是一棵树 $\Leftrightarrow G$ 是无回路的连通图 $\Leftrightarrow G$ 是有 $n-1$ 条边的连通图。其中， $n$ 是顶点个数。

只需在DFS 遍历时，“顺便”记录可能访问到的顶点数和边数，若一趟 DFS 就能访问到 $n$ 个点和 $n-1$ 条边则说明是树。

♾️查找从结点 $v$ 到结点 $u$ 的所有简单路径

只需在DFS 遍历时有回溯地将 visited[] 还原，遍历完所有可能即可。

广/深度优先生成树

无论是广度优先还是深度优先搜索，其搜索过程都可以得到一棵图的遍历树，我们称为 广度优先生成树或深度优先生成树。

应当注意，若是邻接矩阵存储，则生成树唯一；若是邻接表存储，则生成树不唯一。
还应注意，如果图并非连通图，则可能得到的是生成森林而非生成树。

对于无向图来说，广度优先生成树对应着无权图的单源最短路径，所以其树高是所有生成树中最小的；而深度优先生成树是尽可能深地搜索，所以其树高只会大于或等于广度优先生成树。

计算机中的图-基本概念|数据结构Ⅳ

图的基本概念

有向图与无向图

相邻与度数

简单图与完全图

补图与反图

路径与连通

途径、路径和环

无向图的连通性

有向图的连通性

子图与正则图

割点与割边/桥

稀疏图与稠密图

其他特殊的图

图的存储

直接存边法

邻接矩阵

邻接矩阵的幂

邻接表

十字链表

邻接多重表

图的遍历

广度优先遍历

编程实现

BFS 的图应用(部分)

深度优先遍历

编程实现

DFS 的图应用(部分)

广/深度优先生成树

参考