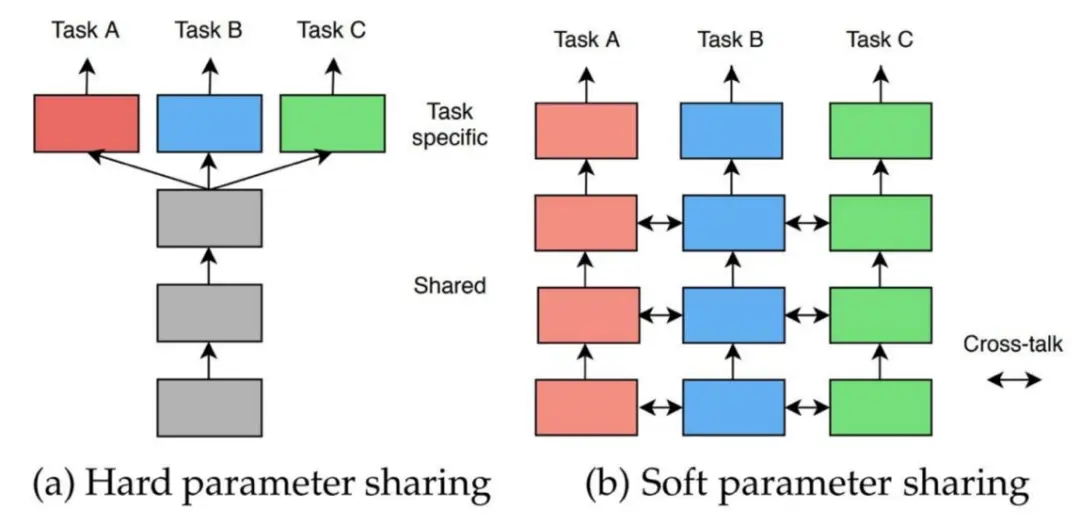
广义表与矩阵压缩|数据结构Ⅰ.2
矩阵压缩
矩阵在计算机图形学、工程机算中占有举足轻重的地位。在数据结构中我们主要关心的是如何利用最小的存储空间来存储同样的一组数据。
- 特殊矩阵 指具有许多相同元素或者零元素,并且这些元素的分布具有一定规律的矩阵。常见的特殊矩阵有:对称矩阵、上(下)三角矩阵、对角矩阵等。
- 特殊矩阵的压缩方法 将特殊矩阵的相同元素的分布规律找出,并设法将其以更小的存储空间映射表示,实现压缩。
对称矩阵
若对于一个 阶方阵 中任一元素 有: 则称 为对称矩阵。
我们可以将其划分为三个部分:上三角区、主对角线、下三角区。
不难发现,对于对称矩阵来说,其上三角区的所有元素都是和下三角区的对应元素相等的,如果我们利用二维数组来存储对称矩阵就会浪费一半的空间,因此,我们可以根据对称矩阵的特性,利用一维数组 存储。
如下图所示,根据对应关系,我们可以将 .
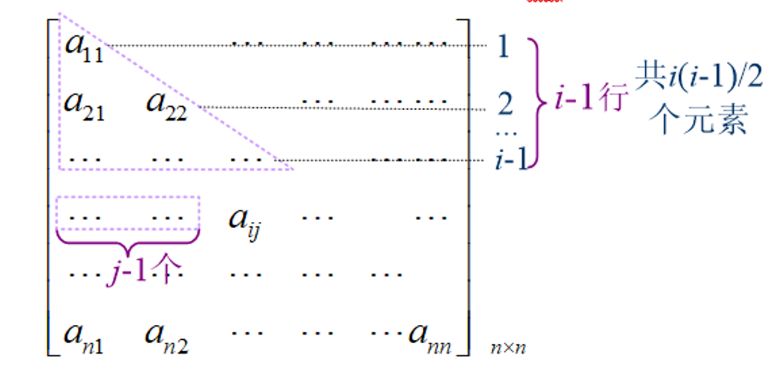
于是有:
注:此处是以数组按下标从
0开始得出的推导
三角矩阵
如图所示,下三角矩阵就是指其上三角区所有元素都是零或者同一常量的矩阵,而上三角矩阵也是对应的定义。

对下三角矩阵压缩的存储思想也和对称矩阵类似,不同之处在于,我们存储完下三角的不同元素的内容之后,还需增设一个空间来保存上三角区的常量(如图)
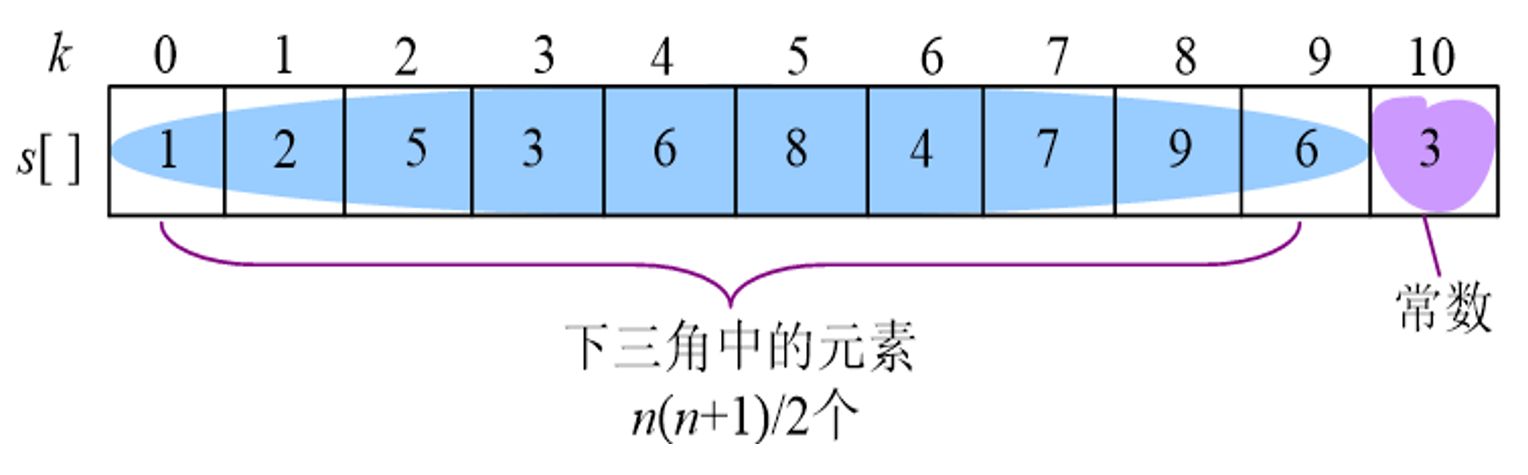
所以,对于下三角矩阵,有:
而对于上三角矩阵,有:
其推导示意图如下: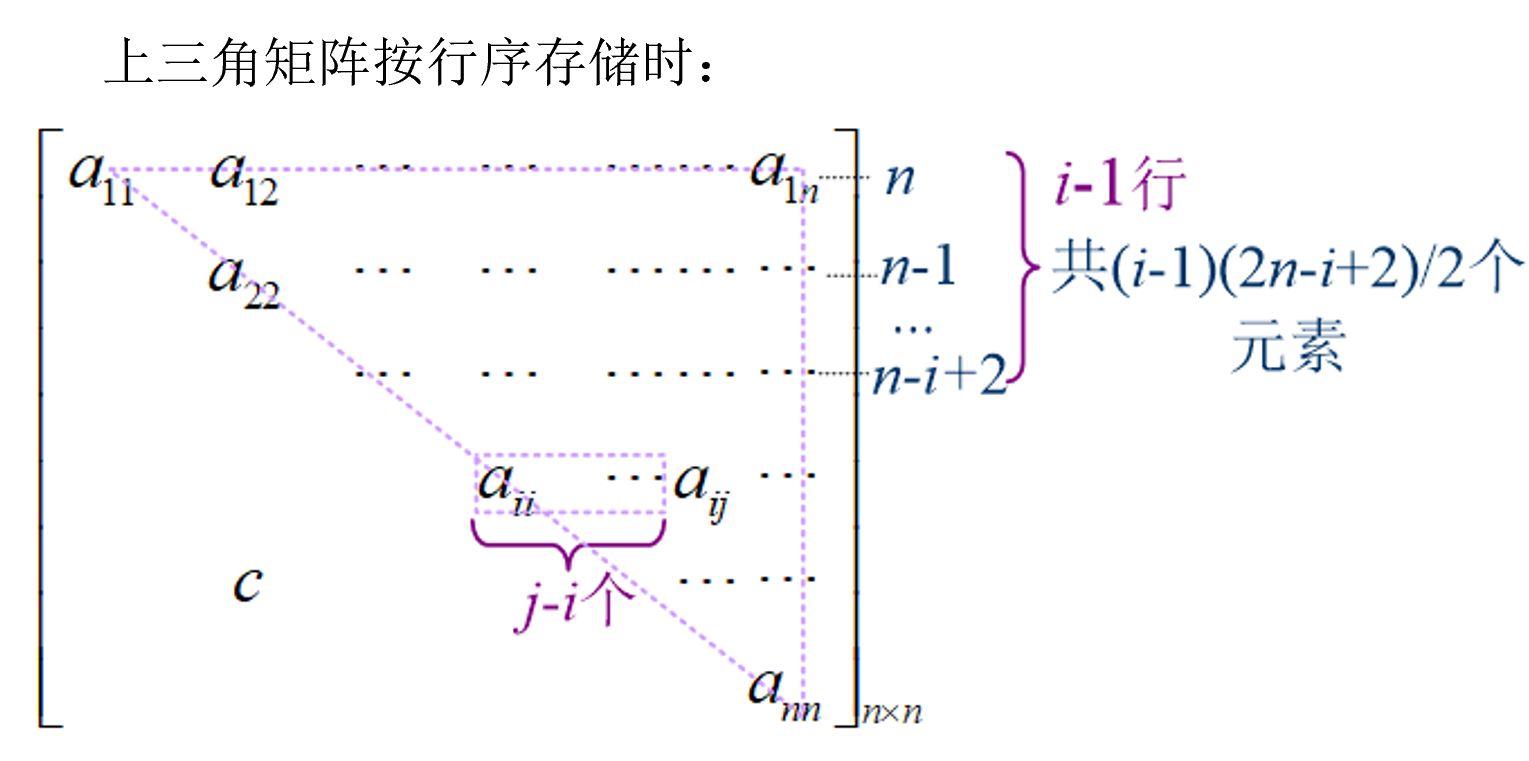
对角矩阵
对角矩阵又称带状矩阵。是指在 阶方阵中,非零元素集中在主对角线及其两侧。
即对任一元素 当 时有. 记 为(奇数),则所得矩阵就是含有 条对角线的带状区域内才有值的矩阵,称为 对角矩阵。
常见的带状矩阵是三对角矩阵。如下图所示:

将 条对角线上的元素按行优先方式存储在一维数组中,为了节省空间,第一行前面和最后一行后面的 个 可以不存储(即 “掐头去尾”),就一共需要 个空间。
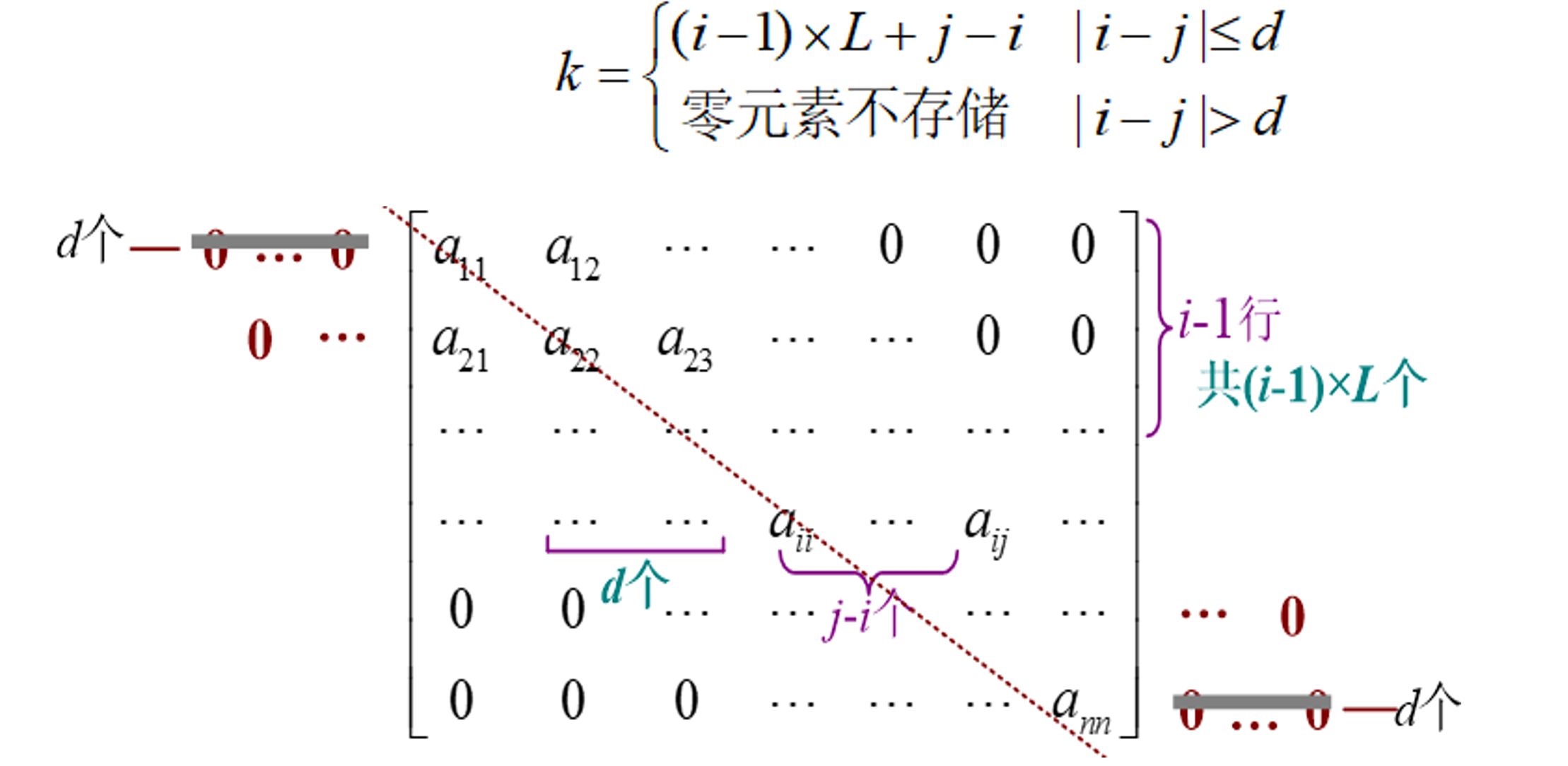
从而对于三对角矩阵, 的下标 满足.
我们也可以由 反解出:
稀疏矩阵
矩阵中非零元素个数 极少,而且分布也不规律,如果非零元素个数只占矩阵元素总数 的25%~30% 或更低时(此时),这样的矩阵称为稀疏矩阵。
如果用传统存储方式,抑或上面我们介绍的压缩方法,都不能更好地节省存储空间,更不必说稀疏矩阵不一定有规律。
系数矩阵的压缩存储一般有两类:三元组顺序表(顺序结构)和十字链表(链式结构)。
三元组
我们考虑只存储非零元素,因为稀疏矩阵无规律性,我们最好还存储非零元素的行数和列数。这样一来我们就得到一个 三元组(行标/cow、列标/col、值/value)。