引例:硬币模型
单硬币抛掷
假设某个盒子里有一枚硬币,抛掷该硬币只有两种结果,即正面(Head,H)和背面(Tail,T)。对抛硬币进行N 次独立重复实验,其中正面朝上的概率设为p 。记正面朝上为1,背面朝上为0,就不难得出每一次抛硬币的结果X∈{0,1} 且服从于二项分布,即Pr{X=x}=px(1−p)1−x,其中p 是未知参数。
换句话说,我们将问题建模出了一个含参的概率模型,我们的目的就是求出这个参数。统计学知识告诉我们对参数p 的估计p^ 可以通过极大似然估计(Maximum Likelihood Estimate,MLE)求得。对上述问题来说可以通过最大化似然函数求得参数:
p^=argpmaxi=1∏Npxi(1−p)1−xi
通常我们可以采用取对数的方法简化求解过程,从而可以记目标函数为l(p) :
l(p)=logpi=1∑Nxi+log(1−p)i=1∑N(1−xi)=Nxˉlogp+N(1−xˉ)log(1−p)
令dl(p)/dp=0 解得p^=xˉ ,是正面朝上占总试验次数的比例。
双硬币抛掷
现假设盒子中有A,B 两枚硬币,它们正面朝上的概率分别记为θA,θB。以相同的概率随机选择一个硬币,进行抛硬币实验,共做N=5 次,每次实验独立的抛十次,结果如下图所示。
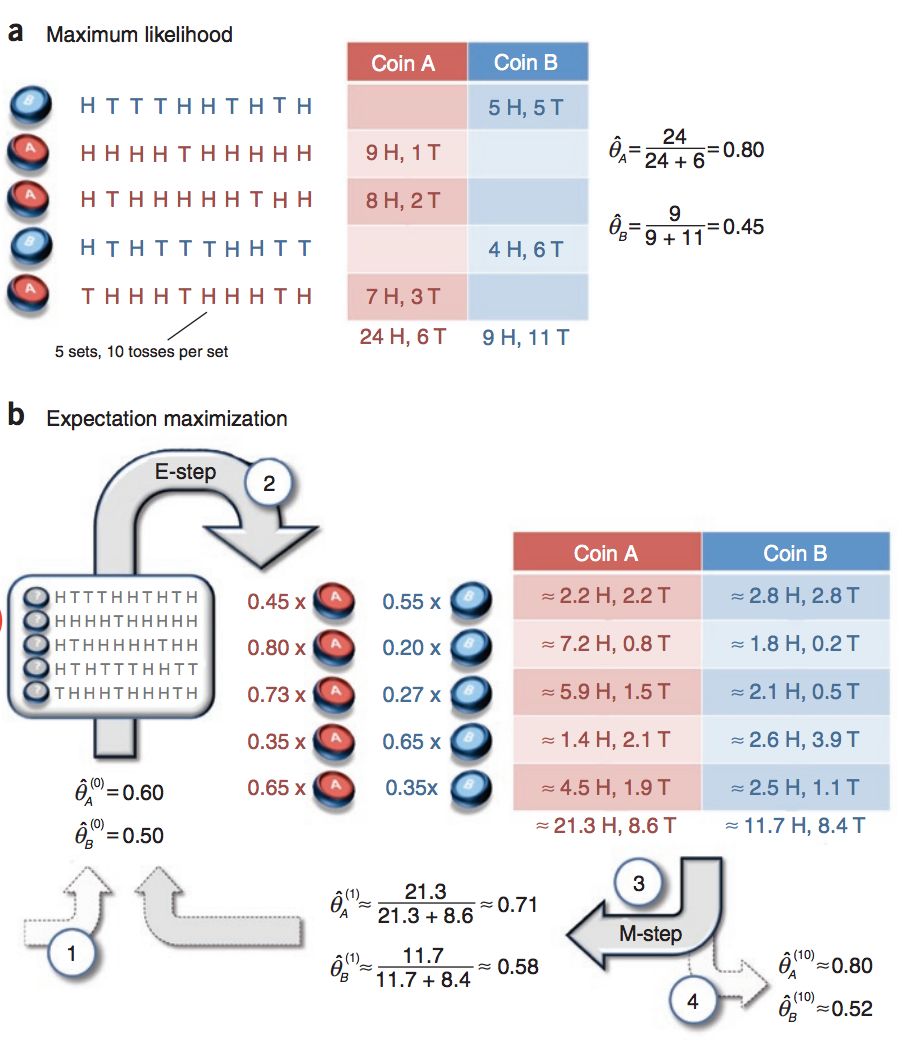
显然,在明确知道每一次实验抛的是A 还是B 的情况下,我们可以分别对A,B 利用单硬币抛掷的方法求得参数(图中a所示)。但是,如果每次实验时并不知道抛的是哪一个硬币,那么传统的 MLE 方法就不再适用了。解决这种问题我们可以使用 EM 算法(图中b所示),这就是本文的重点内容。
EM算法及其原理
EM算法,全称为 Expectation Maximization Algorithm,译作最大期望化算法或期望最大算法。它是一种从不完全数据或有数据丢失的数据集或者说含有隐变量(hidden variable)的概率参数模型中求解参数估计的迭代算法。
原理推导
对于观测数据Y 和概率模型的参数Θ ,为求参数原本可通过最大化似然函数求得,或者是最大化通常所使用的对数似然函数(log-likelihood function):
L(Θ;Y)=logP(Y;Θ)
其中分号 (;) 分隔自变量和参数,P(Y;Θ) 是全体观测样本y∈Y 的联合分布,也是全体样本的似然函数。当每个样本都独立时,P(Y;Θ)=∏y∈YP(y;Θ).
而引入隐变量Z 之后,根据概率论的知识我们有:
P(Y;Θ)=Z∑P(Y,Z;Θ)=Z∑[P(Y∣Z;Θ)⋅P(Z;Θ)]
系联合分布P(Y,Z;Θ) 对Y 的边缘分布(离散版本),也是边缘似然(marginal likelihood)。
接下来,我们利用 Jensen不等式,引入一个函数Q(Z) 来重审目标优化函数:
L=logZ∑P(Y,Z;Θ)=logZ∑(Q(Z)⋅Q(Z)P(Y,Z;Θ))=logEQ[Q(Z)P(Y,Z;Θ)]≥Z∑(Q(Z)⋅logQ(Z)P(Y,Z;Θ))=EQ[logQ(Z)P(Y,Z;Θ)]
其中保证∑ZQ(Z)=1 . 事实上,我们可以把Q(Z) 视为隐变量Z 的概率分布,也就是 Jensen 不等式的概率版本(上式灰色部分,可适用于连续型分布的情况,用积分表示)。
显然不等式右边是目标函数的下界,在取等条件下,极大化这个下界就等同于极大化目标函数。并且还可以进一步将与Θ 无关的项摘掉,这并不影响极大化操作:
Θ∗=argΘmaxL=argΘmaxEQ[logQ(Z)P(Y,Z;Θ)]=argΘmaxEQ[logP(Y,Z;Θ)]=argΘmaxZ∑Q(Z)logP(Y,Z;Θ)
值得注意的是,此处的Q 函数是我们人工引入的只与Z 有关的函数,唯有这样上述的推导才是正确的!
而根据 Jensen 不等式,当且仅当Q(Z)P(Y,Z;Θ)=c 为定值时,可以取等。从而我们可以推导确定Q 函数的表达式:
Q(Z)=∑ZP(Y,Z;Θ)P(Y,Z;Θ)=P(Y;Θ)P(Y,Z;Θ)=P(Z∣Y;Θ)
这个表达式与Θ 有关,所以 EM 算法作为一个迭代算法,提出了一个 2-step 操作。在每次迭代时分别对Z 的分布和Θ 的选取进行计算:
- E step (Expectation):固定当前迭代次数t 已得到的参数Θ(t) 计算P(Z∣Y;Θ(t));
- M step (Maximization):固定Z 的分布,最优化目标函数求得当前最优的参数Θ(t+1) ,即Θ(t+1)=argmaxΘL(Θ,Θ(t))
此外算法的收敛性同样需要我们思考:
- EM算法能保证收敛吗?
- EM算法如果收敛,那么能否保证收敛到全局最大值?
详见:机器学习-白板推导系列(十)-EM算法
算法流程
虽然推导看似很复杂,但是我们可以总结出这样一个流程:
- 输入观测样本数据Y ,隐变量数据Z,联合分布(或联合密度函数)P(Y,Z;Θ) 和条件分布(或条件密度函数)P(Z∣Y;Θ) 以及迭代次数T;
- 随机初始化参数的初值Θ(0);
- E步→M步;
- 判断参数是否收敛,否则继续上一步操作。
双硬币抛掷问题

回看双硬币抛掷问题,我们使用 EM 算法来进行求解(图b所示)。
首先是初始化欲估参数θA(0)=0.6,θB(0)=0.5。规定隐变量z 表示当前抛掷的硬币是A 还是B。接下来计算联合分布:
- 第一行观测数据(5个正面5个背面)是A 的概率P(Y1∣z=A)=
非标准多项式分布
ECM 算法
参考
- EM算法 - LeeLIn。 - 博客园
- EM算法原理总结 - 刘建平Pinard - 博客园
- EM算法及其推广-码农场
- 机器学习-白板推导系列(十)-EM算法(Expectation Maximization)学习笔记 - 知乎