GDLBE - 一种可利用动态特征的出行需求预测
📑 原始论文:Coupling graph deep learning and spatial-temporal influence of built environment for short-term bus travel demand prediction
🌊 项目地址:URAI-Urban-Analytic-and-Intelligence/GDLBE
摘要
基于耦合图深度学习和建成环境时空影响的公交短期出行需求预测
准确且稳健的短期公交出行预测有助于运营公交车队、提供舒适且灵活的公交服务。
建成环境,包括土地利用、各种建筑物以及公共设施,对公交出行需求预测有着重要的影响。
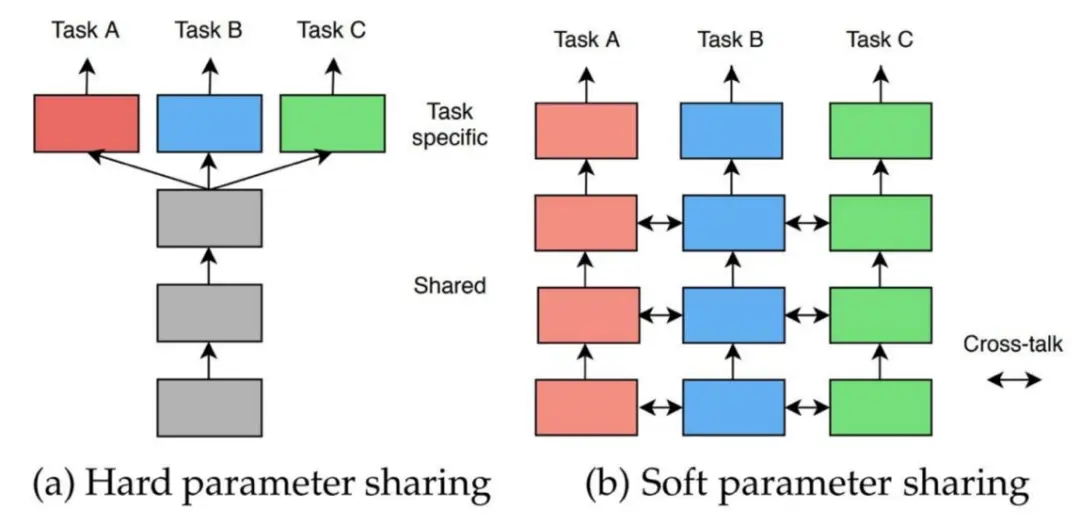
然而,以往的研究将建筑环境视为一种静态特征,在深度学习框架中甚至忽略了建成环境对公交出行的影响。所以,为了填补这一空缺,我们提出了一种基于图深度学习的方法(GDLBE),结合建成环境的时空影响来提高短期公交出行需求预测。
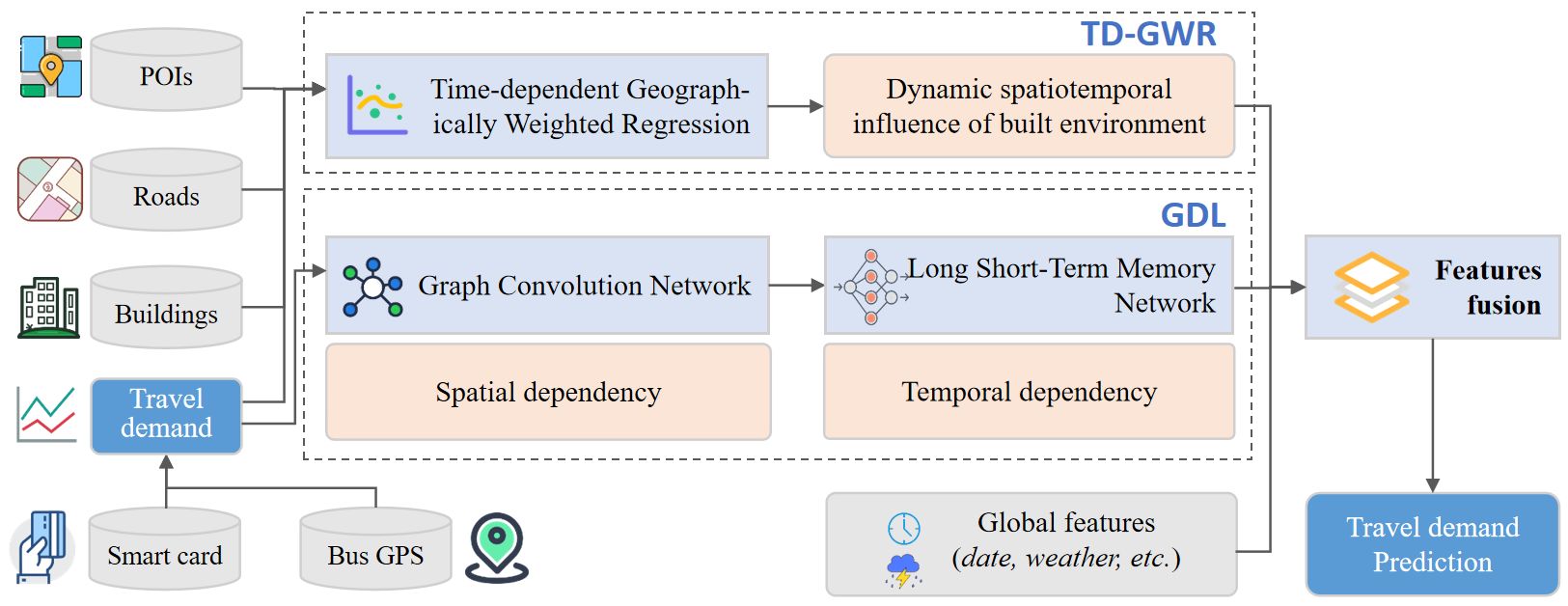
- 采用 时间依赖地理加权回归方法(TD-GWR),解决了建成环境对一天中不同时段公交出行需求的动态影响;
- 利用 图深度学习(GDL) 模块(文章中是 GCN+LSTM)获取大规模公交出行需求背后的综合时空依赖关系;
- 融合动态建成环境影响和时空相关性,对公交短期出行需求进行预测。
问题发现
时空依赖性 |Temporal & Spatial Dependency
对于本问题来说,时间依赖性是指由于人类流动性(mobility)所具有的固有特性,公交出行需求量在一段时间后会出现反复的动态变化。
有研究指出,这类时间依赖性问题可以通过循环神经网络RNN (Recurrent Neural Network) 处理。
Zhao, L., Song, Y., Zhang, C., Liu, Y., Wang, P., Lin, T., Deng, M., & Li, H. (2019). T-GCN: A temporal graph convolutional network for traffic prediction. IEEE Transactions on Intelligent Transportation Systems, 21, 3848–3858.
对于本问题来说,空间依赖性是指公交出行需求受到的由区域周边环境的影响,这些影响都来源于这些地理空间分布信息。
有研究指出,这类空间依赖性问题可以通过卷积神经网络CNN (Convolutional Neural Network) 和图卷积网络 (GCN) 处理。
相关指标:莫兰指数 Morans’ I
Guo, G., & Zhang, T. (2020). A residual spatio-temporal architecture for travel demand forecasting. Transportation Research Part C: Emerging Technologies, 115, Article 102639.
Schlichtkrull, M., Kipf, T. N., Bloem, P., Van Den Berg, R., Titov, I., & Welling, M. (2018). Modeling relational data with graph convolutional networks. In European Semantic Web Conference (pp. 593–607). Springer.
动态建成环境因素
各类建成环境,如:土地利用、建筑物、道路网和兴趣点 ( point-of-interest,POI ) 等,也是影响公交出行需求的因素。

此外,也有各项研究表明,建成环境对公交出行需求的影响会随着时间的变化有所变化,这既是其动态性为出行需求预测带来的困难。在已有的做预测的研究中,也鲜有将这种动态性考虑进去的方法。
方法介绍
形式化
将市政公路生成的维诺图(Voronoi Diagram)视为一个个街道单元(Street-level-units,SLUs),从而进行预测。
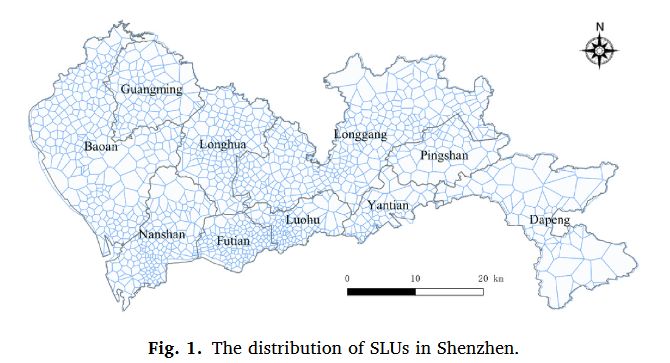
定义图 来表示 SLU 之间的连接关系,其中 为邻接矩阵, 为 SLU 的个数。从而,公交出行需求量的预测问题可以这样表述:
输入:过去 个时间段的历史数据, 是输入特征的维数
输出:接下来 时间段内的,第一个 SLU 到 第 个 SLU 的需求量
时间依赖地理加权回归 |TD-GWR
首先对建成环境和最终的需求量进行预处理:最小最大归一化。
然后,针对各个 SLU 的地理位置信息(坐标:)在 这个时间段的需求 来建立回归模型(矩阵形式):
对于一个加权回归模型来说,其参数估计为:
其中, 是针对第 个 SLU 的空间权重矩阵,他的设计将影响到回归结果。
本文采用 SLU 到 的距离的双平方函数作为权重,即:
以 赤池信息量准则(Akaike Information Criterion,AIC)作为拟合准则进行参数学习。
图深度学习 |GDL
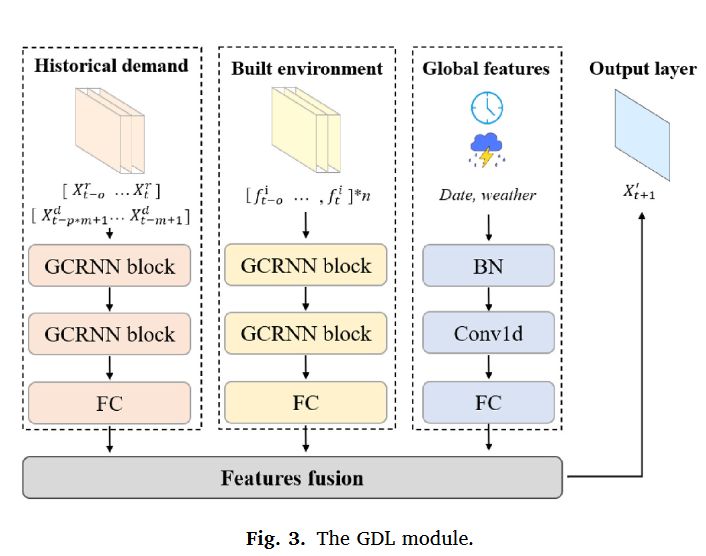
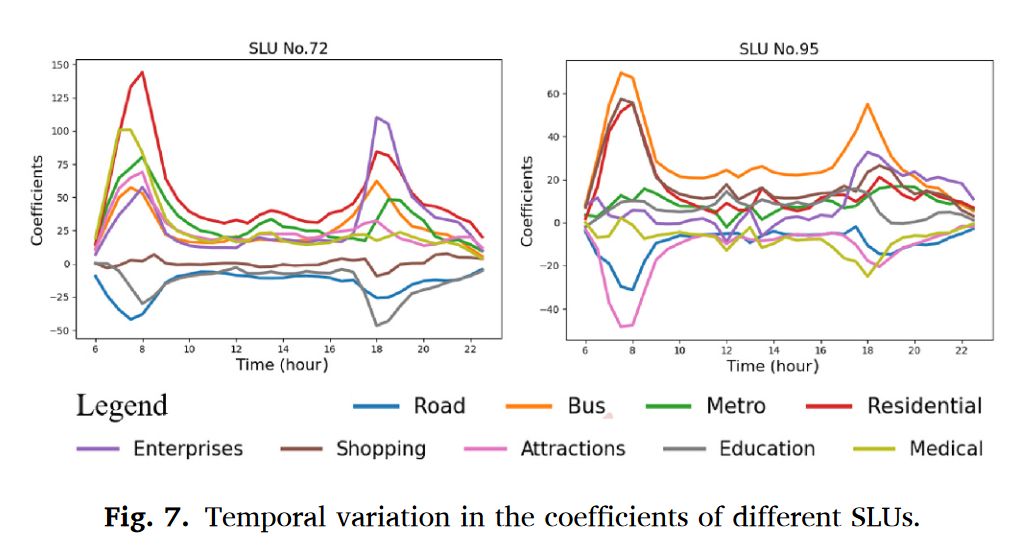
- 短时需求和日需求
- TD-GWR的回归系数(※)
- 全局特征,独热编码进行预处理,BN归一化
三者通过全连接层(FC)进行缩放统一,最后通过 Features fusion 进行加权统合:
评估时,将输出结果rescale到原始范围(※),以 MSE 作为损失函数。
GCRNN
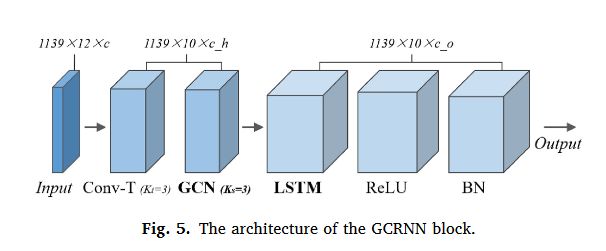
- Conv-T 和 LSTM 用于捕捉时间依赖性。
- GCN用来捕捉空间依赖性。
思考
回归系数的使用
文中利用时间的地理加权回归方法,本来可以直接得到建成环境在特定时间段与出行需求量的一个拟合关系,当然效果不一定很好。在笔者的常规思路里,可能会直接把 GWR 的输出作为一个特征,用于后续计算,但是本文却是将学习得到的回归系数(也就是线性表达式中某个自变量的系数)作为特征参与后续计算。
这里面,GWR充当的角色其实是提取出某种建成环境(自变量)的“重要性”,或数值上的一种信息,将其作为特征参与后续计算,或许能更好地改善模型效果。
输出结果的rescale
文章表示最后的输出结果是经过 函数得到的,其取值在,最后再将其缩放到需求量的范围,然后再和实际值计算残差/Loss。
这里笔者表示有点困惑,因为无法界定什么是“需求量的范围”,如果是把历史数据的需求量范围作为参考的话,这种操作缺乏一定的合理性,因为缩放过程中最大也只能到历史数据的最大值,对现实情况的预测效果可能是一种阻碍。