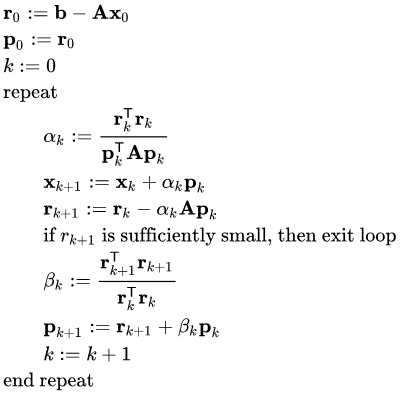前言 在 【最优化】非线性优化及KKT条件 一文中,我们介绍了非线性优化问题的必要条件和充分条件,通过这些最优性条件,我们可以在数学上和理论上求解到显性的或者解析的最优解。但现实中待优化的目标函数可能较为复杂,并且考虑到希望利用计算机来求解的工程场景,基于迭代 的方法来求出最优解不失为最佳的选择。
本文将着眼于无约束的非线性最优化问题:
min f ( x ) , x ∈ R n \min\;f(\boldsymbol x),\quad\boldsymbol x\in\Bbb R^n min f ( x ) , x ∈ R n
其中,f ( x ) f(\boldsymbol x) f ( x ) R n \Bbb R^n R n 一阶连续偏导数 的实函数 。
介绍基于目标函数的导数 ,通过一系列一维搜索/线搜索 (见文末附赠章节),不断迭代最终达到最优值的方法。这类方法的核心思想总是:希望从某一点出发,选择一个使得当前目标函数值下降最快的方向对起始点进行更新,以尽快到达极小点。
最速下降法 最速下降法(steepest descent )最早由法国数学家 Augustin-Louis Cauchy1 在 1847 年提出,Jacques Hadamard 也于 1907 年独立地提出了一种类似的方法。在 1944 年Haskell Curry 首次研究了该方法在非线性优化问题中的收敛性 ,此后该方法得到了越来越多的研究和应用。
最速下降方向 最速下降法的核心思想是找到在当前点x \boldsymbol x x f ( x ) f(\boldsymbol x) f ( x ) d \boldsymbol d d d \boldsymbol d d D f ( x ; d ) \text{D}f(\boldsymbol x;\boldsymbol d) D f ( x ; d )
D f ( x ; d ) = ∇ f ( x ) ⊤ d \text{D}f(\boldsymbol x;\boldsymbol d)=\nabla f(\boldsymbol x)^\top\boldsymbol d D f ( x ; d ) = ∇ f ( x ) ⊤ d
所以,要找到下降最快的方向等价于最小化 方向导数。由于只是找方向(对其模长不做要求),因此不是一般性地,我们可以约束∥ d ∥ ≤ 1 \Vert\boldsymbol d\Vert\leq1 ∥ d ∥ ≤ 1
min ∇ f ( x ) ⊤ d s.t. ∥ d ∥ ≤ 1 \begin{aligned} \min \quad&\nabla f(\boldsymbol x)^\top\boldsymbol d\\ \text{s.t.}\quad&\Vert\boldsymbol d\Vert\leq1 \end{aligned} min s.t. ∇ f ( x ) ⊤ d ∥ d ∥ ≤ 1
【求解】利用 Schwartz 不等式:
∣ ∇ f ( x ) ⊤ d ∣ ≤ ∥ ∇ f ( x ) ∥ ∥ d ∥ ≤ ∥ ∇ f ( x ) ∥ |\nabla f(\boldsymbol x)^\top\boldsymbol d|\leq\Vert\nabla f(\boldsymbol x)\Vert\ \Vert\boldsymbol d\Vert\leq\Vert\nabla f(\boldsymbol x)\Vert ∣∇ f ( x ) ⊤ d ∣ ≤ ∥∇ f ( x ) ∥ ∥ d ∥ ≤ ∥∇ f ( x ) ∥
去掉绝对值,有
∇ f ( x ) ⊤ d ≥ − ∥ ∇ f ( x ) ∥ \nabla f(\boldsymbol x)^\top\boldsymbol d\geq-\Vert\nabla f(\boldsymbol x)\Vert ∇ f ( x ) ⊤ d ≥ − ∥∇ f ( x ) ∥
从而当
d = − ∇ f ( x ) ∥ ∇ f ( x ) ∥ \boldsymbol d=-\frac{\nabla f(\boldsymbol x)}{\Vert\nabla f(\boldsymbol x)\Vert} d = − ∥∇ f ( x ) ∥ ∇ f ( x )
成立时,方向导数最小,从而函数值下降最快。
因为模长对方向没有影响,所以可以下结论:负梯度方向就是最速下降方向 。
🔔上述推导中假设了约束中的范数为欧氏范数 ,而在其他度量空间下时最速下降方向的表达式就会发生变化,不一定再是负梯度方向。例如在A \bf A A ∥ d ∥ A = ( d ⊤ A d ) 1 / 2 \Vert\boldsymbol d\Vert_{\bf A}=(\boldsymbol d^\top\mathbf A\boldsymbol d)^{1/2} ∥ d ∥ A = ( d ⊤ A d ) 1/2
当取 欧氏范数/L 2 L2 L 2 梯度下降法 。
最速下降算法步骤 最速下降法从初始点x ( 1 ) \boldsymbol x^{(1)} x ( 1 ) d ( k ) \boldsymbol d^{(k)} d ( k ) λ k \lambda_k λ k x ( k + 1 ) = x ( k ) + λ k d ( k ) \boldsymbol x^{(k+1)}=\boldsymbol x^{(k)}+\lambda_k\boldsymbol d^{(k)} x ( k + 1 ) = x ( k ) + λ k d ( k )
其中的步长因子λ k \lambda_k λ k 一维搜索 。令φ ( λ ) = f ( x ( k ) + λ d ( k ) ) \varphi(\lambda)=f(\boldsymbol x^{(k)}+\lambda\boldsymbol d^{(k)}) φ ( λ ) = f ( x ( k ) + λ d ( k ) )
λ k = arg min λ φ ( λ ) \lambda_k=\arg\min_{\lambda}\varphi(\lambda) λ k = arg λ min φ ( λ )
整个算法步骤如下:
此处的步长因子在梯度下降法领域被称为学习率 ,常用η \eta η 【最优化】梯度下降算法及其变体总结
锯齿现象 容易证明,用最速下降法极小化目标函数时,相邻的两个搜索方向是正交的。说明如下:
在搜索最优步长时,理想情况下为极小化φ ( λ ) \varphi(\lambda) φ ( λ ) φ ′ ( λ ) = 0 \varphi'(\lambda)=0 φ ′ ( λ ) = 0 λ k \lambda_k λ k
φ ′ ( λ ) = ∇ f ( x ( k ) + λ d ( k ) ) ⊤ ⋅ d ( k ) = 0 ⇒ ∇ f ( x ( k + 1 ) ) ⊤ ⋅ d ( k ) = 0 / / ∵ x ( k + 1 ) = x ( k ) + λ k d ( k ) ⇒ d ( k + 1 ) ⊤ ⋅ d ( k ) = 0 / / ∵ d ( k + 1 ) = − ∇ f ( x ( k + 1 ) ) \begin{aligned} \varphi'(\lambda)&=\nabla f(\boldsymbol x^{(k)}+\lambda\boldsymbol d^{(k)})^\top\cdot\boldsymbol d^{(k)}=0\\\\ \Rightarrow &\nabla f(\boldsymbol x^{(k+1)})^\top\cdot\boldsymbol d^{(k)}=0\quad \color{teal}//\because \boldsymbol x^{(k+1)}=\boldsymbol x^{(k)}+\lambda_k\boldsymbol d^{(k)}\\ \Rightarrow &{\boldsymbol d^{(k+1)}}^\top\cdot\boldsymbol d^{(k)}=0\quad\color{teal}//\because \boldsymbol d^{(k+1)}=-\nabla f(\boldsymbol x^{(k+1)}) \end{aligned} φ ′ ( λ ) ⇒ ⇒ = ∇ f ( x ( k ) + λ d ( k ) ) ⊤ ⋅ d ( k ) = 0 ∇ f ( x ( k + 1 ) ) ⊤ ⋅ d ( k ) = 0 // ∵ x ( k + 1 ) = x ( k ) + λ k d ( k ) d ( k + 1 ) ⊤ ⋅ d ( k ) = 0 // ∵ d ( k + 1 ) = − ∇ f ( x ( k + 1 ) )
这表明迭代产生的序列{ x ( k ) } \{\boldsymbol x^{(k)}\} { x ( k ) } x ( k ) \boldsymbol x^{(k)} x ( k ) 锯齿现象 (zigzagging phenomenon)尤为明显,这影响了算法是收敛效率。
综上所述,最速下降法反映了目标函数的一种局部性质。局部上看,最速下降方向对当前的搜索有利;但全局上看,向着极小点移动的过程中需要经历不少弯路,收敛速率越来越慢。因此,最速下降法更适用于计算过程的前期迭代部分或间插步骤。
Lemaréchal, C. (2012). “Cauchy and the Gradient Method” (PDF). Doc Math Extra: 251–254.
共轭梯度法 共轭梯度法(conjugate gradient method )最早由 Magnus Hestenes 和 Eduard Stiefel 在1952 年提出。一开始它是用于特定线性方程组——系数矩阵为对称正定阵的线性方程组A x = b \bf Ax=b Ax = b
之后,共轭梯度法被发现还可用于求解无约束优化问题,现已成为了一种重要的最优化方法。
共轭方向 设A A A n × n n\times n n × n ∃ d ( 1 ) , d ( 2 ) ∈ R n \exists \;\boldsymbol{d}^{(1)},\boldsymbol{d}^{(2)}\in\Bbb R^n ∃ d ( 1 ) , d ( 2 ) ∈ R n d ( 1 ) ⊤ A d ( 2 ) = 0 {\boldsymbol{d}^{(1)}}^\top A\boldsymbol{d}^{(2)}=0 d ( 1 ) ⊤ A d ( 2 ) = 0 A A A 共轭 。
若∃ d ( 1 ) , d ( 2 ) , . . , d ( k ) ∈ R n \exists \;\boldsymbol{d}^{(1)},\boldsymbol{d}^{(2)},..,\boldsymbol{d}^{(k)}\in\Bbb R^n ∃ d ( 1 ) , d ( 2 ) , .. , d ( k ) ∈ R n A A A A A A A A A k k k 共轭方向 。若它们均为非零向量,则它们构成的向量组线性无关 。
共轭梯度算法原理 共轭梯度法在最优化问题上的思想是将共轭性与最速下降法 结合,利用已知点出的梯度构造一组共轭方向,然后沿着这组方向进行搜索 。
共轭梯度法由两个部分组成:(1)一维搜索最优λ k \lambda_k λ k f f f β k \beta_k β k d \boldsymbol d d
d ( k + 1 ) = − g k + 1 + β k d ( k ) \boldsymbol d^{(k+1)}=-\boldsymbol g_{k+1}+\beta_k\boldsymbol d^{(k)} d ( k + 1 ) = − g k + 1 + β k d ( k )
其中,g k = d e f ∇ f ( x ( k ) ) \boldsymbol g_k\xlongequal{\rm def}\nabla f(\boldsymbol x^{(k)}) g k def ∇ f ( x ( k ) )
现在我们先考虑二次凸函数 问题:
min f ( x ) = d e f 1 2 x ⊤ A x + b ⊤ x + c \min\;f(\boldsymbol x)\xlongequal{\rm def}\frac12\boldsymbol x^\top A\boldsymbol x+\boldsymbol b^\top\boldsymbol x+c min f ( x ) def 2 1 x ⊤ A x + b ⊤ x + c
其中A A A
第一部分 和最速下降法一样,我们先确定步长因子。令φ ′ ( λ ) = 0 \varphi'(\lambda)=0 φ ′ ( λ ) = 0
φ ′ ( λ ) = ∇ f ( x ( k ) + λ d ( k ) ) ⊤ ⋅ d ( k ) = [ A ( x ( k ) + λ d ( k ) ) + b ] ⊤ ⋅ d ( k ) / / ∵ ∇ f = A x + b = [ g k + λ A d ( k ) ] ⊤ ⋅ d ( k ) = 0 \begin{aligned} \varphi'(\lambda)&=\nabla f(\boldsymbol x^{(k)}+\lambda\boldsymbol d^{(k)})^\top\cdot\boldsymbol d^{(k)}\\ &=[A(\boldsymbol x^{(k)}+\lambda\boldsymbol d^{(k)})+\boldsymbol b]^\top\cdot\boldsymbol d^{(k)}\quad \color{teal}//\because \nabla f=A\boldsymbol x+\boldsymbol b\\ &=[\boldsymbol g_k+\lambda A\boldsymbol d^{(k)}]^\top\cdot\boldsymbol d^{(k)}\\&=0 \end{aligned} φ ′ ( λ ) = ∇ f ( x ( k ) + λ d ( k ) ) ⊤ ⋅ d ( k ) = [ A ( x ( k ) + λ d ( k ) ) + b ] ⊤ ⋅ d ( k ) // ∵ ∇ f = A x + b = [ g k + λ A d ( k ) ] ⊤ ⋅ d ( k ) = 0
可以解得
λ k = − g k ⊤ d ( k ) d ( k ) ⊤ A d ( k ) \begin{aligned} \lambda_k=-\frac{\boldsymbol g_k^\top\boldsymbol d^{(k)}}{\boldsymbol d^{(k)\top} A\boldsymbol d^{(k)}} \end{aligned} λ k = − d ( k ) ⊤ A d ( k ) g k ⊤ d ( k )
这个λ k \lambda_k λ k
第二部分 将方向更新公式d ( k + 1 ) = − g k + 1 + β k d ( k ) \boldsymbol d^{(k+1)}=-\boldsymbol g_{k+1}+\beta_k\boldsymbol d^{(k)} d ( k + 1 ) = − g k + 1 + β k d ( k ) d ( k ) ⊤ A {\boldsymbol d^{(k)}}^\top A d ( k ) ⊤ A
d ( k ) ⊤ A d ( k + 1 ) = − d ( k ) ⊤ A g k + 1 + β k d ( k ) ⊤ A d ( k ) {\boldsymbol d^{(k)}}^\top A\boldsymbol d^{(k+1)}=-{\boldsymbol d^{(k)}}^\top A\boldsymbol g_{k+1}+\beta_k{\boldsymbol d^{(k)}}^\top A\boldsymbol d^{(k)} d ( k ) ⊤ A d ( k + 1 ) = − d ( k ) ⊤ A g k + 1 + β k d ( k ) ⊤ A d ( k )
为了让d ( k + 1 ) \boldsymbol d^{(k+1)} d ( k + 1 ) d ( k ) \boldsymbol d^{(k)} d ( k )
β k = − d ( k ) ⊤ A g k + 1 d ( k ) ⊤ A d ( k ) \beta_k=-\frac{\boldsymbol d^{(k)\top} A\boldsymbol g_{k+1}}{\boldsymbol d^{(k)\top} A\boldsymbol d^{(k)}} β k = − d ( k ) ⊤ A d ( k ) d ( k ) ⊤ A g k + 1
前提条件 可以证明,当初始 搜索方向d ( 1 ) \boldsymbol d^{(1)} d ( 1 ) − g 1 -\boldsymbol g_1 − g 1 A A A 如果初始方向不遵循最速下降法的选取方式,FR法得到的后继方向就未必共轭!!
对一般函数 推广到任意函数f ( x ) f(\boldsymbol x) f ( x ) λ k \lambda_k λ k A A A ∇ 2 f ( x ( k ) ) \nabla^2f(\boldsymbol x^{(k)}) ∇ 2 f ( x ( k ) ) 二阶 Taylor 展开式近似 为一个二次凸函数推导得来的。
此外,对应一般函数往往共轭梯度法不能直接在有限步求得极小点,所以算法中往往会添加一个重置判断 ,达到重置条件时重新用当前最速下降方向作为迭代方向,而不再是用共轭梯度法的更新公式。
最后我们得到下列所示的计算步骤(来自:Open Problems in Nonlinear Conjugate Gradient Algorithms for Unconstrained Optimization | Semantic Scholar
图中的α k \alpha_k α k λ k \lambda_k λ k β \beta β
对于二次凸函数作为目标函数的情况时,以上表达式均是等价 的!但在应对一般函数时,性能有所差别。
牛顿法 牛顿法(Newton’s method )最初由英国科学家艾萨克·牛顿(Isaac Newton)在17世纪提出,首次发表于 1685 年 John Wallis 的《历史与实用代数论》(A Treatise of Algebra both Historical and Practical)中,用于求解多项式方程的根 。
1690 年,约瑟夫·拉夫逊(Joseph Raphson)在《普遍等式分析》(Analysis aequationum universalis)一书中给出了更加简化的描述 。虽然他也只将该方法应用于多项式,但他从原始多项式中提取了每个连续修正,从而避免了牛顿原始方法繁琐的重写过程,从而为每个问题推导出一个可重复使用的迭代表达式。因此牛顿法有时也被称为牛顿-拉夫逊方法(Newton-Raphson method )。
最后,1740 年,托马斯·辛普森(Thomas Simpson)将牛顿法描述为一种使用微积分求解一般非线性方程的迭代方法,辛普森还将牛顿法推广到了二元方程组,并指出牛顿法可以通过将梯度设为零来解决优化问题 。
牛顿法求根 在数值分析 中,牛顿法可以用于求出一元可微函数的零点(方程的根)的数值解。
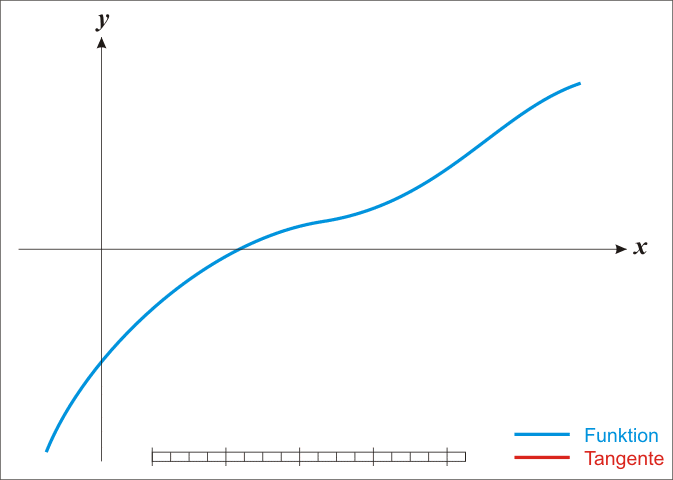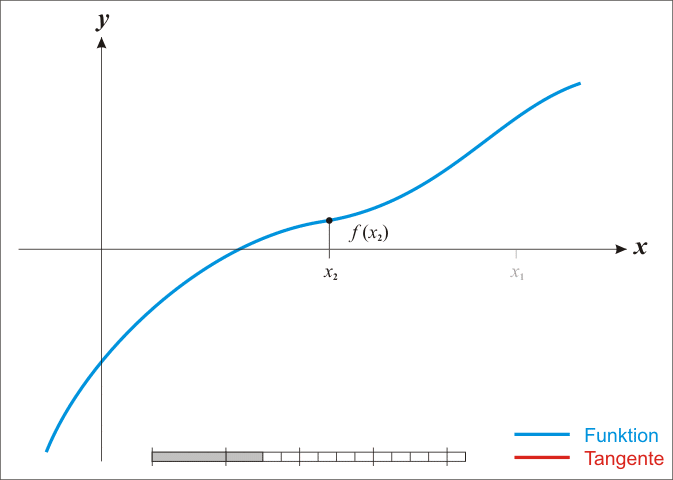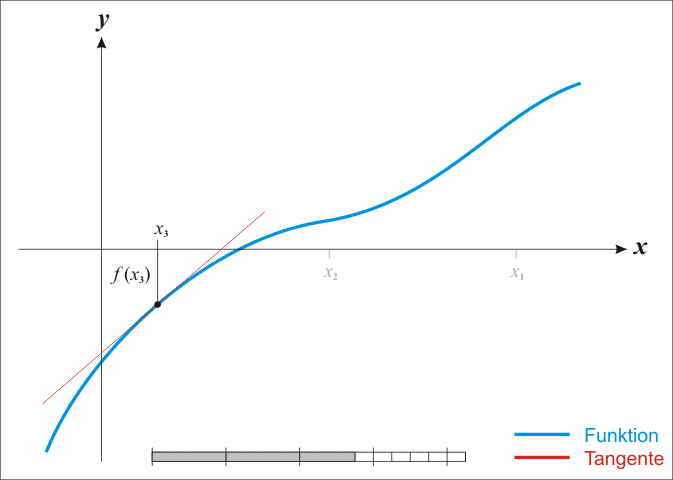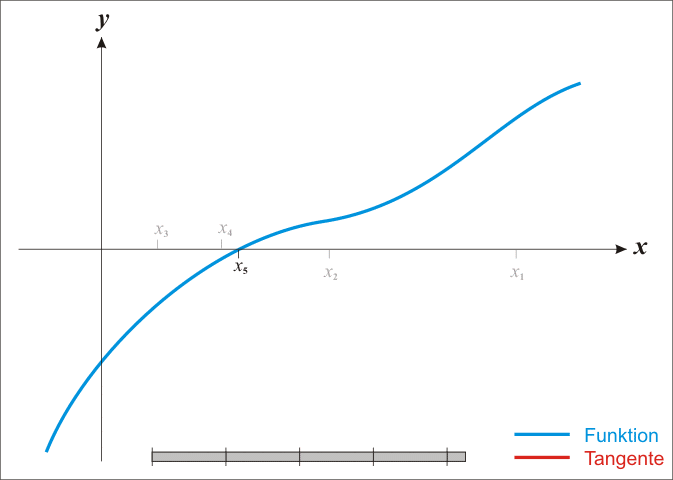
首先,选取一个接近函数f ( x ) f(x) f ( x ) x 0 x_0 x 0 f ( x 0 ) f(x_0) f ( x 0 ) f ′ ( x 0 ) f'(x_0) f ′ ( x 0 ) f ′ ( x 0 ) f'(x_0) f ′ ( x 0 ) ( x 0 , f ′ ( 0 ) ) (x_0,f'(0)) ( x 0 , f ′ ( 0 )) x x x ( x 1 , 0 ) (x_1,0) ( x 1 , 0 ) x 1 x_1 x 1 x 0 x_0 x 0 x ∗ ( f ( x ∗ ) = 0 ) x^*\quad(f(x^*)=0) x ∗ ( f ( x ∗ ) = 0 )
上述过程实际上就等价于求解下列方程:
0 = ( x − x 0 ) ⋅ f ′ ( x 0 ) + f ( x 0 ) 0=(x-x_0)·f'(x_0)+f(x_0) 0 = ( x − x 0 ) ⋅ f ′ ( x 0 ) + f ( x 0 )
解得
x 1 = x 0 − f ( x 0 ) f ′ ( x 0 ) x_1=x_0-\frac{f(x_0)}{f'(x_0)} x 1 = x 0 − f ′ ( x 0 ) f ( x 0 )
接下来,为了找到零点更精确的值,我们再用同样的方法从x 1 x_1 x 1 x 2 , x 3 , . . . x_2,x_3,... x 2 , x 3 , ...
事实上,这个方法等价于在x 0 x_0 x 0 近似 看作一次函数。这个近似由Taylor展开式 忽略高阶项得出:
f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) = d e f φ ( x ) f(x)\approx f(x_0)+f'(x_0)(x-x_0)\xlongequal{\rm def}\varphi(x) f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) def φ ( x )
此时令φ ( x ) = 0 \varphi(x)=0 φ ( x ) = 0 x 1 x_1 x 1 k k k
x k = x k − 1 − f ( x k − 1 ) f ′ ( x k − 1 ) x_k=x_{k-1}-\frac{f(x_{k-1})}{f'(x_{k-1})} x k = x k − 1 − f ′ ( x k − 1 ) f ( x k − 1 )
优化中的牛顿法 在最优化领域,我们往往需要通过令可微函数的导数为零求其极值点。事实上求“导函数为零的点”就等价于求解“导函数的零点/方程的根”。
所以对于二阶可导的一元函数,我们可以利用牛顿法 得到极值点的更新公式。
推广之,对于多元二次可微实函数 f ( x ) f(\boldsymbol x) f ( x )
f ( x ) ≈ ϕ ( x ) = f ( x ( k ) ) + ∇ f ( x ( k ) ) ⊤ ( x − x ( k ) ) + 1 2 ( x − x ( k ) ) ⊤ ∇ 2 f ( x ( k ) ) ( x − x ( k ) ) f(\boldsymbol x)\approx\phi(\boldsymbol x)=f(\boldsymbol x^{(k)})+\nabla f(\boldsymbol x^{(k)})^\top(\boldsymbol x-\boldsymbol x^{(k)})+\frac12(\boldsymbol x-\boldsymbol x^{(k)})^\top\nabla^2 f(\boldsymbol x^{(k)})(\boldsymbol x-\boldsymbol x^{(k)}) f ( x ) ≈ ϕ ( x ) = f ( x ( k ) ) + ∇ f ( x ( k ) ) ⊤ ( x − x ( k ) ) + 2 1 ( x − x ( k ) ) ⊤ ∇ 2 f ( x ( k ) ) ( x − x ( k ) )
其中,∇ 2 f ( x ( k ) ) \nabla^2 f(\boldsymbol x^{(k)}) ∇ 2 f ( x ( k ) )
令∇ ϕ ( x ) = 0 \nabla\phi(\boldsymbol x)=\bf0 ∇ ϕ ( x ) = 0
x ( k + 1 ) = x ( k ) − ∇ 2 f ( x ( k ) ) − 1 ∇ f ( x ( k ) ) \boldsymbol x^{(k+1)}=\boldsymbol x^{(k)}-\nabla^2 f(\boldsymbol x^{(k)})^{-1}\nabla f(\boldsymbol x^{(k)}) x ( k + 1 ) = x ( k ) − ∇ 2 f ( x ( k ) ) − 1 ∇ f ( x ( k ) )
整个算法流程如下图所示:
二次终止性 对于n n n f ( x ) = 1 2 x ⊤ A x + b ⊤ x + c f(\boldsymbol x)=\frac12\boldsymbol x^\top A\boldsymbol x+\boldsymbol b^\top\boldsymbol x+c f ( x ) = 2 1 x ⊤ A x + b ⊤ x + c ∇ f ( x ) = 0 \nabla f(\boldsymbol x)=\bf0 ∇ f ( x ) = 0 x ∗ = − A − 1 b \boldsymbol x^*=-A^{-1}\boldsymbol b x ∗ = − A − 1 b
而当我们利用牛顿法来求解该问题时,任取一个初点x ( 1 ) \boldsymbol x^{(1)} x ( 1 )
x ( 2 ) = x ( 1 ) − ∇ 2 f ( x ( 1 ) ) − 1 ∇ f ( x ( 1 ) ) = x ( 1 ) − A − 1 ( A x ( 1 ) + b ) = − A − 1 b \begin{aligned} \boldsymbol x^{(2)}&=\boldsymbol x^{(1)}-\nabla^2 f(\boldsymbol x^{(1)})^{-1}\nabla f(\boldsymbol x^{(1)})\\ &=\boldsymbol x^{(1)}-A^{-1}(A\boldsymbol x^{(1)}+\boldsymbol b)\\ &=-A^{-1}\boldsymbol b \end{aligned} x ( 2 ) = x ( 1 ) − ∇ 2 f ( x ( 1 ) ) − 1 ∇ f ( x ( 1 ) ) = x ( 1 ) − A − 1 ( A x ( 1 ) + b ) = − A − 1 b
可以发现,正好就是最优解。这说明牛顿迭代法具有二次终止性 (也称二次收敛性)。
D e f i n e : \bf Define: Define : n n n f ( x ) = 1 2 x ⊤ A x + b ⊤ x + c f(\boldsymbol x)=\frac12\boldsymbol x^\top A\boldsymbol x+\boldsymbol b^\top\boldsymbol x+c f ( x ) = 2 1 x ⊤ A x + b ⊤ x + c 迭代 算法能从任意点出发,经过有限步迭代达到最优解,则称该算法具有二次终止性 。
我们可以下结论:最速下降法不具备二次终止性,而共轭梯度法具有二次终止性 。
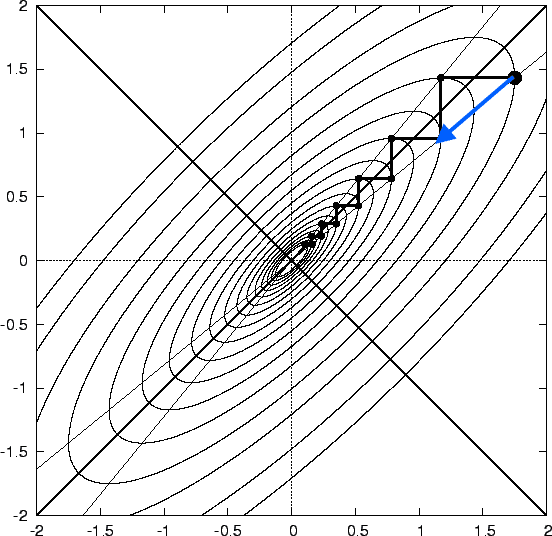
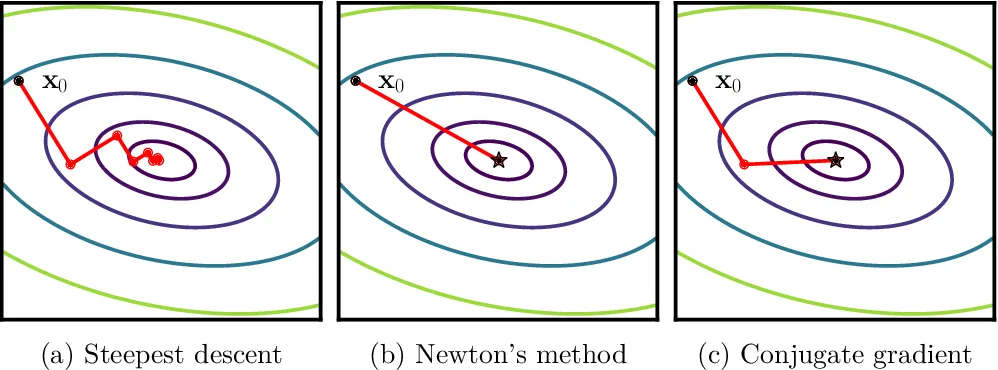
此外,牛顿法在极小点附近具有很快的收敛速度,避免了最速下降法的锯齿现象。上述三种算法的收敛可视化如下图所示:
阻尼牛顿法 在使用牛顿迭代法求解最优化问题时,有一点值得注意:当初始点远离极小点时,牛顿法可能不收敛。
记牛顿方向d = − ∇ 2 f ( x ( k ) ) − 1 ∇ f ( x ( k ) ) \boldsymbol d=-\nabla^2 f(\boldsymbol x^{(k)})^{-1}\nabla f(\boldsymbol x^{(k)}) d = − ∇ 2 f ( x ( k ) ) − 1 ∇ f ( x ( k ) ) x ( k + 1 ) = x ( k ) + d ( k ) \boldsymbol x^{(k+1)}=\boldsymbol x^{(k)}+\boldsymbol d^{(k)} x ( k + 1 ) = x ( k ) + d ( k )
因此,阻尼牛顿法 (Damped Newton’s Method)提了出来,和最速下降法和共轭梯度法一样引入了可一维搜索的步长因子λ k \lambda_k λ k λ k → 0 \lambda_k\to0 λ k → 0
修正牛顿法 虽然阻尼牛顿法解决了原始牛顿法的一些问题,但是它们仍然拥有共同的缺点:
可能出现 Hesse 矩阵 是奇异 的情况,因其不可逆使更新公式失效; Hesse 矩阵未必正定,此时牛顿方向未必下降,阻尼牛顿算法也会失效(λ = 0 \lambda=0 λ = 0 x \boldsymbol x x 为解决上述问题,修正牛顿法 (Modified Newton’s Method)提出构造 一个对称正定矩阵 B k B_k B k ∇ 2 f ( x ( k ) ) \nabla^2 f(\boldsymbol x^{(k)}) ∇ 2 f ( x ( k ) )
构造B k B_k B k
B k = ∇ 2 f ( x ( k ) ) + ϵ k I B_k=\nabla^2 f(\boldsymbol x^{(k)})+\epsilon_k\boldsymbol I B k = ∇ 2 f ( x ( k ) ) + ϵ k I
I \boldsymbol I I n n n ϵ k \epsilon_k ϵ k α k \alpha_k α k ϵ k \epsilon_k ϵ k B k B_k B k α k + ϵ k \alpha_k+\epsilon_k α k + ϵ k
最后我们给出修正牛顿法的算法描述:
拟牛顿法 牛顿法最突出的特点就是收敛速度很快,但是它需要计算二阶偏导数,并且 Hesse 矩阵可能非正定。修正牛顿法虽然解决了 Hesse 矩阵的非正定问题,但是对目标函数的二阶可微性、计算二阶偏导数的计算代价 仍然有要求。为此,一类提出直接使用与二阶导数无关 的矩阵来近似 牛顿法中的∇ 2 f ( x ( k ) ) − 1 \nabla^2 f(\boldsymbol x^{(k)})^{-1} ∇ 2 f ( x ( k ) ) − 1 拟牛顿法 。
拟牛顿条件 为构造∇ 2 f ( x ( k ) ) − 1 \nabla^2 f(\boldsymbol x^{(k)})^{-1} ∇ 2 f ( x ( k ) ) − 1 G k G_k G k ∇ 2 f ( x ( k ) ) − 1 \nabla^2 f(\boldsymbol x^{(k)})^{-1} ∇ 2 f ( x ( k ) ) − 1
设在第k k k x ( k + 1 ) \boldsymbol x^{(k+1)} x ( k + 1 )
f ( x ) ≈ f ( x ( k + 1 ) ) + ∇ f ( x ( k + 1 ) ) ⊤ ( x − x ( k + 1 ) ) + 1 2 ( x − x ( k + 1 ) ) ⊤ ∇ 2 f ( x ( k + 1 ) ) ( x − x ( k + 1 ) ) f(\boldsymbol x)\approx f(\boldsymbol x^{(k+1)})+\nabla f(\boldsymbol x^{(k+1)})^\top(\boldsymbol x-\boldsymbol x^{(k+1)})+\frac12(\boldsymbol x-\boldsymbol x^{(k+1)})^\top\nabla^2 f(\boldsymbol x^{(k+1)})(\boldsymbol x-\boldsymbol x^{(k+1)}) f ( x ) ≈ f ( x ( k + 1 ) ) + ∇ f ( x ( k + 1 ) ) ⊤ ( x − x ( k + 1 ) ) + 2 1 ( x − x ( k + 1 ) ) ⊤ ∇ 2 f ( x ( k + 1 ) ) ( x − x ( k + 1 ) )
进而梯度∇ f ( x ) ≈ ∇ f ( x ( k + 1 ) ) + ∇ 2 f ( x ( k + 1 ) ) ( x − x ( k + 1 ) ) \nabla f(\boldsymbol x)\approx \nabla f(\boldsymbol x^{(k+1)})+\nabla ^2f(\boldsymbol x^{(k+1)})(\boldsymbol x-\boldsymbol x^{(k+1)}) ∇ f ( x ) ≈ ∇ f ( x ( k + 1 ) ) + ∇ 2 f ( x ( k + 1 ) ) ( x − x ( k + 1 ) )
接下来取x = x ( k ) \boldsymbol x=\boldsymbol x^{(k)} x = x ( k ) s ( k ) = x ( k + 1 ) − x ( k ) , y ( k ) = ∇ f ( x ( k + 1 ) ) − ∇ f ( x ( k ) ) \boldsymbol s^{(k)}=\boldsymbol x^{(k+1)}-\boldsymbol x^{(k)}, \boldsymbol y^{(k)}=\nabla f(\boldsymbol x^{(k+1)})-\nabla f(\boldsymbol x^{(k)}) s ( k ) = x ( k + 1 ) − x ( k ) , y ( k ) = ∇ f ( x ( k + 1 ) ) − ∇ f ( x ( k ) )
y ( k ) ≈ ∇ 2 f ( x ( k + 1 ) ) s ( k ) \boldsymbol y^{(k)}\approx\nabla^2 f(\boldsymbol x^{(k+1)})\boldsymbol s^{(k)} y ( k ) ≈ ∇ 2 f ( x ( k + 1 ) ) s ( k )
当 Hesse 可逆时,s ( k ) ≈ ∇ 2 f ( x ( k + 1 ) ) − 1 y ( k ) \boldsymbol s^{(k)}\approx\nabla^2 f(\boldsymbol x^{(k+1)})^{-1}\boldsymbol y^{(k)} s ( k ) ≈ ∇ 2 f ( x ( k + 1 ) ) − 1 y ( k )
于是,如果我们需要找到一个矩阵G k + 1 G_{k+1} G k + 1 逆 ,相当于它需要满足下列等式:
s ( k ) = G k + 1 y ( k ) \boldsymbol s^{(k)}=G_{k+1}\boldsymbol y^{(k)} s ( k ) = G k + 1 y ( k )
这个公式也被叫做拟牛顿条件 (Secant equation).
构造近似矩阵 满足拟牛顿条件的 矩阵G k G_{k} G k G 1 G_1 G 1 n n n I I I 矫正矩阵 Δ G k \Delta G_k Δ G k G k G_k G k G k + 1 G_{k+1} G k + 1
G k + 1 = G k + Δ G k G_{k+1}=G_k+\Delta G_k G k + 1 = G k + Δ G k
接下来就是如何设计矫正矩阵了。不同的算法有着不同的设计方式。
秩一矫正 我们知道一个n n n n n n
Δ G k = α k z ( k ) z ( k ) ⊤ \Delta G_k=\alpha_k\boldsymbol z^{(k)}{\boldsymbol z^{(k)}}^\top Δ G k = α k z ( k ) z ( k ) ⊤
其中,α k \alpha_k α k z ( k ) \boldsymbol z^{(k)} z ( k ) n n n
将这样的矫正矩阵带入拟牛顿条件,可以得到
Δ G k = ( s ( k ) − G k y ( k ) ) ( s ( k ) − G k y ( k ) ) ⊤ y ( k ) ⊤ ( s ( k ) − G k y ( k ) ) \Delta G_k=\frac{(\boldsymbol s^{(k)}-G_k\boldsymbol y^{(k)})(\boldsymbol s^{(k)}-G_k\boldsymbol y^{(k)})^\top}{\boldsymbol y^{(k)\top}(\boldsymbol s^{(k)}-G_k\boldsymbol y^{(k)})} Δ G k = y ( k ) ⊤ ( s ( k ) − G k y ( k ) ) ( s ( k ) − G k y ( k ) ) ( s ( k ) − G k y ( k ) ) ⊤
DFP算法 DFP算法是拟牛顿法中一种著名的算法,由 Davidon 首先提出,后经 Fletcher 和 Powell 改进,DFP的命名取自他们三人的名字 Davidon-Fletcher-Powell 。 该算法也被称为 变尺度法 。
DFP 设计矫正矩阵如下:
Δ G k = α k u ( k ) u ( k ) ⊤ + β k v ( k ) v ( k ) ⊤ \Delta G_k=\alpha_k\boldsymbol u^{(k)}{\boldsymbol u^{(k)}}^\top+\beta_k\boldsymbol v^{(k)}{\boldsymbol v^{(k)}}^\top Δ G k = α k u ( k ) u ( k ) ⊤ + β k v ( k ) v ( k ) ⊤
并且,取u ( k ) = s ( k ) , v ( k ) = G k y ( k ) \boldsymbol u^{(k)}=\boldsymbol s^{(k)},\;\boldsymbol v^{(k)}=G_k\boldsymbol y^{(k)} u ( k ) = s ( k ) , v ( k ) = G k y ( k ) α k = 1 / s ( k ) ⊤ y ( k ) \alpha_k=1/{\boldsymbol s^{(k)}}^\top\boldsymbol y^{(k)} α k = 1/ s ( k ) ⊤ y ( k ) β k = 1 / y ( k ) ⊤ G k y ( k ) \beta_k=1/{\boldsymbol y^{(k)}}^\top G_k\boldsymbol y^{(k)} β k = 1/ y ( k ) ⊤ G k y ( k )
最后得到
Δ G k = s ( k ) s ( k ) ⊤ s ( k ) ⊤ y ( k ) − G k s ( k ) ( G k s ( k ) ) ⊤ y ( k ) ⊤ G k y ( k ) \Delta G_k=\frac{\boldsymbol s^{(k)}\boldsymbol s^{(k)\top}}{\boldsymbol s^{(k)\top}\boldsymbol y^{(k)}}-\frac{G_k\boldsymbol s^{(k)}(G_k\boldsymbol s^{(k)})^\top}{\boldsymbol y^{(k)\top} G_k\boldsymbol y^{(k)}} Δ G k = s ( k ) ⊤ y ( k ) s ( k ) s ( k ) ⊤ − y ( k ) ⊤ G k y ( k ) G k s ( k ) ( G k s ( k ) ) ⊤
Broyden族 前面我们提到的G k G_k G k ∇ 2 f ( x ( k ) ) − 1 \nabla^2 f(\boldsymbol x^{(k)})^{-1} ∇ 2 f ( x ( k ) ) − 1 B k B_k B k ∇ 2 f ( x ( k ) ) \nabla^2 f(\boldsymbol x^{(k)}) ∇ 2 f ( x ( k ) )
类似的方法我们有B k + 1 = B k + Δ B k B_{k+1}=B_k+\Delta B_k B k + 1 = B k + Δ B k y ( k ) = B k + 1 s ( k ) \boldsymbol y^{(k)}=B_{k+1}\boldsymbol s^{(k)} y ( k ) = B k + 1 s ( k )
显然,要找到一个Δ B k \Delta B_k Δ B k Broyden–Fletcher–Goldfarb–Shanno (BFGS ) algorithm 。
有研究表明,BFGS 和 DFP 的加权线性组合仍然满足拟牛顿公式,权重选取不同得到的修正公式就不同,全体的修正公式被称为Broyden族 。
此外还有其他的设计方法:
信赖域方法 待更
附赠:一维搜索 待更