模型的解释分析与特征可视化
前言
随着机器学习的发展,模型的准确性变得越来越高,但对应的可解释性却在下降。特别是随着神经网络的发展而兴起的各类深度学习模型也面临着准确率和可解释性的矛盾。由此,所谓机器学习的可解释性(Interpretability)或解释模型(Explainable AI, XAI) 也慢慢在机器学习的研究中占领一席之地。
关于模型解释性,除了线性模型和决策树这种天生就具备很好解释性的模型以外,其他复杂的模型都面临着解释性的困难。因此,一系列将输出归因于输入特征的归因分析(Attribution Analysis) 方法以及对中间层进行可视化的方法被提出,皆在对深度网络模型进行“后天”解释。
关于这些方法的代码及其使用可跳转到本文 Captum 一节
LRP
📃On Pixel-Wise Explanations for Non-Linear Classifier Decisions by Layer-Wise Relevance Propagation
Layer-wise Relevance Propagation (LRP) 是一种基于层间交互的归因方法,同时也是一个由一组约束定义出来的概念,因此任何满足约束的解决方案都可以被认为遵循了LRP概念的方法。
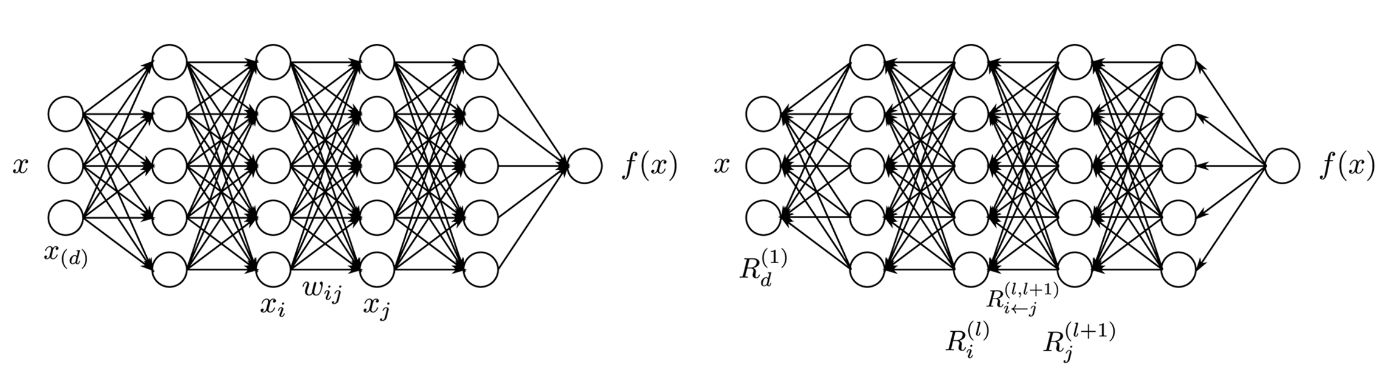
如图所示,具体来说,LRP是一种从输出回溯到输入的反向过程,认为网络层中每一层所有维度(所有神经元)的相关性之和均相等并且等于输出值。可以由下列公式表出:
其中, 表示第 个神经元属于第 层, 表示第 层网络第 个神经元的关联度。
并且,认为第 层的某个神经元 的关联度等于第 层中所有和它连接的神经元的关联度之和。即:
其中, 表示从 层回溯到 层时,神经元 与神经元 连接的中间关联度。一般来说,可以通过网络中 层各分量对第 层的神经元 的总量占比作为系数来衡量这个中间关联度的值,如:
具体根据不同的激活函数还有所调整,实际应用中还有 规则和 规则等变体,具体可查看原论文。
DeepLIFT
📃 Learning Important Features Through Propagating Activation Differences
DeepLIFT 是一种将模型的输出变化归因于输入特征的变化的方法。和常见的归因方法类似, DeepLIFT 也是通过设计某种量化的公式来衡量不同输入特征对输出的贡献度,从而实现解释模型的目的。它的“创新点”在于是使用了“变化”的概念,在数学上就是考虑输入和输出的变化量 和.
具体来说,人为设定某种“参考(reference)”输入 和“参考”输出。然后定义:
指定输出的变化量 是由依赖于每个分量变化量 的贡献量 累加得到的。
Multiplier
类比梯度 及链式法则,作者定义乘数 并赋予其链式法则。即,对于含有 个中间层 的深层网络,最终输出对输入的乘数满足:
贡献分数规则
为了更进一步提供完备的可解释性,作者还给出了区分正负贡献的规则,有:
然后是对贡献分数的计算,作者针对线性层(用于Dense层,卷积层等)和非线性层(如ReLU,tanh 或 Sigmoid 等)都采取不同的公式。
下面仅简要介绍规则内容,具体公式较长,详见原论文。
- 线性规则:由 得出 ,再根据其正负划分;
- Rescale规则:对非线性层 ,考虑记 ,然后考虑特殊情况后划分,解决了梯度饱和的问题;
- RevealCancel规则:在上述非线性层规则的基础上,进一步区分正负贡献设计公式,保证了特征间的依赖性。
Integrated Gradients
📃Axiomatic Attribution for Deep Networks
积分梯度 (Integral Gradients,IGs) 是一种结合了直接梯度 、LRP 和 DeepLIFT 的归因技术。文章作者针对现实问题提出了两个公理,敏感性 (Sensitivity) 和 实现不变性 (Implementation Invariance),说明了传统方法不能保证两种公理同时成立,最后提出了 IGs。
敏感性
选取两个不同的输入值(相对于基线值而言)时,模型应该输出不同的预测,这样子该特征将被赋予非零归因。换言之,所使用的基于梯度的方法应该保证计算出来的贡献值是对输入值的变化敏感的。
实现不变性
尽管内部实现不一致,但对于所有的输入,输出结果都是一致的两个模型被称为是功能等效的。面对两个功能等效的模型进行归因分析而获得相同的成因的归因算法满足实现不变性。因为这才能真正保证可以将输出值归结于输入,与算法内部的实现路径脱敏。
显然 LRP 和 DeepLIFT 内部的算法因为高度依赖网络设计,所以是不满足该公理的。
直接梯度
对于深度网络而言,输出对输入的直接梯度 (Gradients) 直接反应了模型的输入对输出的动力学影响,理论上是归因分析最自然的量化指标。
从而,模型的标量输出 对输入向量 中的每一个分量 的直接梯度
就可以直接代表该分量的贡献度。
很明显在非线性激活函数普遍被用于网络结构中的当下,该方法不可避免地存在梯度饱和的阶段(例如 ReLU 函数)。在该阶段内梯度趋向于零,这表明输入的变化几乎不会影响输出值。这也说明直接梯度法是不满足公理1的敏感性的。
积分梯度法
积分梯度法参考了 DeepLIFT 的思路,当给定一个基值 base value(对应 DeepLIFT 的 reference)时,第 个输入特征的贡献度可以用输出对它的梯度求积分表示:
接下来我们给出具体的推导。
设 是由输入到输出的映射,那么输出的变化量可以根据牛顿莱布尼茨公式得到:
进一步地,可以对每一个分量根据定积分的加法法则可以进行拆分:
这样一来,我们就可以认为累加计算中的每一项都代表着各个分量的贡献度了。最后,为了对上式进行一个优雅的标准化,我们还可以引入一个路径函数 代表连接两个点 的曲线,保证.
利用换元法,令 就有:
特别地,当积分路径是一条直线时,就有:. 该经典积分路径满足轮换对称性,具有优良性质。于是上式就可以化简成前面给出的一般形式了。
考虑利用计算机来进行积分计算的有效性,IGs的计算将 通过黎曼近似积分求解:
※ 此处的 这个符号代表的是对 的 分量求梯度,而不是对输入变量中的名为 的这个变量求梯度。 一定要注意区分!!!
显然,IGs 的计算只与输入输出有关,所以满足实现不变性。因为引入了积分的概念,其数值计算时是通过平均 中大量点的梯度得来的,这也就克服了敏感性的问题。有趣的是,作者进一步指出积分的引入甚至满足了完整度(Completeness),一种涵盖了敏感性的更高级的公理说是。
LIME
SHAP
📃 A Unified Approach to Interpreting Model Predictions
SHAP (SHapley Additive exPlanations) 是一种基于代价函数的解释方法,理论上可以解释任何机器学习模型的任何决策。受到博弈论中的 Shapley Value 的启发,SHAP的核心思想是通过计算每个特征在模型决策中的加性贡献度(additive feature attribution),从而解释模型的决策过程。
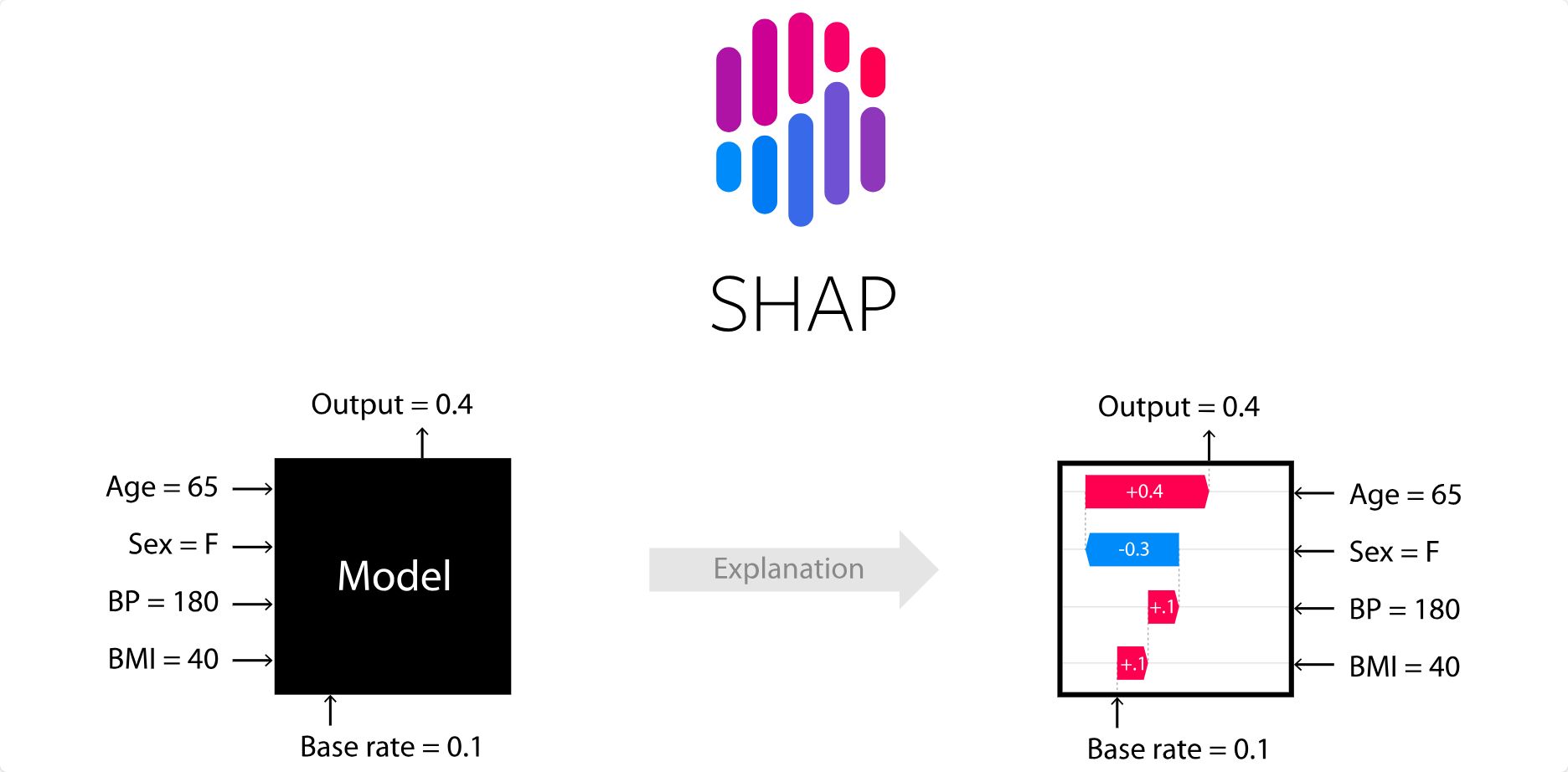
Shapley Value
设想有 个海盗组成了一个团队,在一次成功的探险后获得了 100 个金币,怎么公平地分配呢?平均分配显然不合理,而按照能力分配呢——海盗 A 战力无双就应该多分钱吗?海盗 B 虽然弱不禁风但是唯一的医生,似乎更加不可或缺?
分配规则还有这样一些限制条件:
- 有效性。每个人贡献分数应该相加等于
100,这样才能正好分完100枚金币 - 对称性。如果有两个人价值一样,那么所得也该一样
- 虚拟性。如果有个人可有可无,那么他分配的结果是
0 - 可加性。分配
100金币的结果,应该等于先分配40,再分配60的结果
Shapley Value (夏普利值)被证明是唯一满足上述条件的解,从而海盗 在给定某个价值函数 的情况下的价值分数 可以表示如下:
其中, 是一个价值函数,返回给定集合的价值。 表示所有海盗构成的集合, 表示去除海盗 之后的所有可能的集合, 表示集合 中的海盗成员数量,同理有 表示所有海盗的数量。
更多 Shapley Value 的原理及其推导可参考:
Shapley Value 学习笔记 - lif323 - 博客园
Shapley_Value全解析与公式推导_shapley value-CSDN博客
考虑线性模型
SHAP的定义
Shap库与画图
Welcome to the SHAP documentation — SHAP latest documentation
让 SHAP 输出比优雅更优雅的图表 - 墨天轮 (modb.pro)
基线理解_SHAP的变量解释性绘图理解与应用_shap值的图怎么解释-CSDN博客
SHAP 可视化解释机器学习模型简介_shap图-CSDN博客
Captum
Captum · Model Interpretability for PyTorch
https://github.com/pytorch/captum/issues/308
CAM
万字长文:特征可视化技术(CAM) - 知乎 (zhihu.com)
CV-Tech-Guide/Visualize-feature-maps-and-heatmap: 可视化特征图教程 (github.com)
类别激活图(CAM)可视化 — MMPretrain 1.2.0 文档