序列浅学：循环神经网络及其发展 - RNN

时间序列分析

时间序列是指将同一统计指标的数值按其发生的时间先后顺序排列而成的数列。这些数值通常是在连续的时间间隔内采样得出。
由于时间序列中隐藏着一些过去与未来的关系，因此基于历史数据的模式和趋势，对未来时间点的值进行预测的这种分析方法就油然而生，称之为时间序列分析和预测。

形式化地，预测某指标在时间步 $t$ 时的数值大小 $x_t$ 的途径如下：

$x_t \sim P(x_t \mid x_{t-1}, \ldots, x_1)$

时间序列特征

在时间序列分析中，通常会考虑以下几个时间序列的特征：

趋势（Trend）：时间序列中的长期变化方向，可能是上升、下降或平稳的。
季节性（Seasonality）：时间序列中出现的周期性模式，通常与特定时间间隔（如每周、每月）相关。
周期性（Cyclic Patterns）：时间序列中的波动性，不像季节性那样有固定的时间间隔。
噪声（Noise）：时间序列中的随机波动，可能来自于测量误差或外部因素。

常见预测模型

移动平均法（Moving Average）：使用一定时间窗口内的数据均值来预测未来值。
指数平滑法（Exponential Smoothing）：对历史数据赋予不同权重，以更好地捕捉数据的变化趋势。
自回归模型（Autoregressive Models）：基于过去时间点的值来预测未来时间点的值。
移动平均自回归模型（ARMA）：结合了自回归和移动平均的特点，用于更复杂的数据。
季节性分解法（Seasonal Decomposition）：将时间序列数据分解为趋势、季节性和随机成分，然后对各个分量进行建模和预测。
ARIMA模型（Autoregressive Integrated Moving Average）：结合了自回归、差分和移动平均的元素，适用于具有趋势和季节性的数据。
神经网络模型：例如循环神经网络（RNN）和长短时记忆网络（LSTM），用于捕捉时间序列中的复杂模式。
Prophet模型：由Facebook开发的开源预测模型，专门用于处理时间序列数据，具有易用性和良好的效果。

自回归与隐回归

Autoregression is a time series model that uses observations from previous time steps as input to a regression equation to predict the value at the next time step.

根据自回归模型（Autoregression Model）的思想，很容易理解其本质是将历史数据与当前需要计算的数据进行回归拟合。以线性回归为例，就有：

$x_t=\sum_{i=0}^{t-1}\beta_ix_i+\varepsilon_t$

其中， $\varepsilon_t$ 为随机扰动项，假定为独立同分布的白噪声（通常取高斯噪声）。

显然，当时间足够长时，历史数据就会越来越多，计算代价也会越来越大。而现实中，很多时候未来的走向与很久以前的数据之间关系并不密切（这个内容将在马尔可夫模型一章中继续展开）。所以，出于对训练模型和现实因素的多种考虑，自回归模型通常取一固定的窗口 $p$ 内的历史数据进行拟合。即：

$x_t\sim P(x_t\mid x_{t-1},x_{t-2},...,x_{t-p})$

对应的模型也记为 $AR(p)$ 模型。

除了固定窗口以外，还有一种方法：通过某种特征 $h_t$ 来保留从初始到上一时刻数据的信息，然后利用该特征进行预测。即：

$\hat{x_t}\sim P(x_t\mid h_t)$

然后当获得真实 $x_t$ 后又通过某种方式（比如函数 $g$ ）更新 $h_t$ ，即 $h_{t+1}=g(h_t,\;x_t)$ 。

因为 $h_t$ 并非可以直接观测到的值，它是作为模型中的某种隐藏特征而使用的，所以这种策略的模型也被称为隐变量自回归模型（Latent Autoregressive Models）。

循环神经网络

在深度学习领域我们除了独立特征的数据外，自然也面临着对序列数据的处理问题。比如下面这些序列输入的经典任务：

语音识别（speech recognition）
时间序列预测（time series prediction）
机器翻译（machine translation）

循环神经网络（Recurrent Neural Networks， RNN） 就是这样一类用于处理序列数据的神经网络。RNN 引入了“记忆”的概念，用到了前面我们提到的隐变量自回归模型的思想，即隐状态。

隐状态

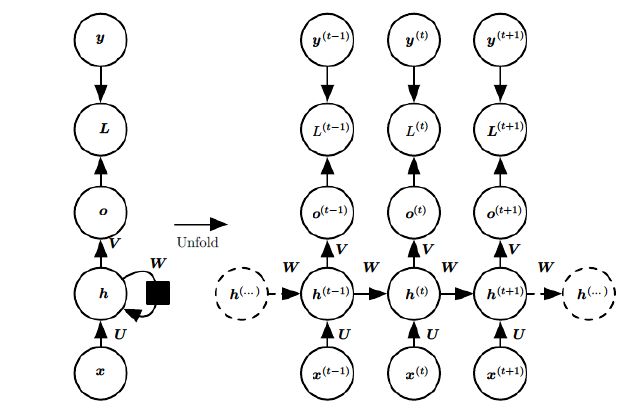
经典RNN模型结构

和隐回归一样，RNN 隐状态的学习依赖于数据自身之前的观测数据，并且对每一个时间步 $t$ 都需要对隐状态 $\boldsymbol h$ 进行更新。如果不按时间序列展开(右图)，直接看其简化流图(左图)，很明显这个更新过程是一种“循环”。所以这一层被称为循环层，神经网络也因此得名循环神经网络。

上图中， $o^{(t)}$ 为在时间步 $t$ 时仅由 $h^{(t)}$ 决定的输出； $L$ 为对应损失函数； $y$ 为真实输出； $U,V,W$ 是神经网络的权重，注意，它们在整个 RNN 中是共享的。

前向传播

对于任意时间步 $t$ ，隐状态 $h^{(t)}$ 由 $x^{(t)}$ 和 $h^{(t-1)}$ 得到：

$h^{(t)}=\sigma(Ux^{(t)}+Wh^{(t-1)}+b)$

其中， $\sigma$ 为 RNN 的激活函数，一般选为 $\tanh$ （后面解释）.

而输出与预测如下：

$\begin{aligned} o^{(t)}&=Vh^{(t)}+c\\ \hat{y}^{(t)}&=\sigma(o^{(t)}) \end{aligned}$

长期依赖

得到前向传播之后，为了优化权重，我们自然需要继续应用神经网络中喜闻乐见的反向传播算法。对于 RNN 这种处理时间序列的神经网络，对应的则是时间反向传播（backpropagation through time，BPTT）。

由于 RNN 需要处理的是大量的时间序列数据，并且共享权重，所以在反向传播求取关于权重的梯度时会受到大数据量的长期依赖，会出现梯度消失或爆炸的问题。

这里我们以没有偏置非常简单的循环结构： $h_t=Wh_{t-1}$ 为例。有：

$\begin{aligned} h_t&=W^th_0\\ \nabla_WL&=\nabla_{h_t}L\cdot\frac{\partial h_t}{\partial W}=h_0tW^{t-1}\nabla_{h_t}L \end{aligned}$

若 $W$ 可以正交分解： $W=Q\varLambda Q^T$ ，则

$\nabla_{W}L=h_0Q\varLambda^{t-1}Q^T\nabla_{h_t}L$

于是随着不断的幂乘，在前向传播中， $h_0$ 在特征值不到1的部分会逐渐衰减到0，大于1的部分会呈指数级增长。在反向传播中，不仅仅对 $\nabla_WL$ ，对其他梯度也有类似的情况。因此不论是前向传播还是反向传播求梯度的过程都会受到影响，更新权重时利用的梯度下降自然也受到严重影响。

对于前向传播而言，如果将激活函数设为 $\tanh(\cdot)$ ，即 $h_t=\tanh(Ux_t+Wh_{t-1}+b)$ ，有：

$\frac{\partial h_t}{\partial h_{t-1}}=\text{diag}(1-(h_t)^2)W$

这将每一时间步的 $h$ 的幅度都被 $\tanh(\cdot)$ 限制在了 $(-1,1)$ 之间。所以前向传播不会指数级增长。这就是 $RNN$ 使用 $\tanh(\cdot)$ 而不是 $\text{ReLU}(\cdot)$ 的原因。

但是对于反向传播而言，梯度爆炸或消失的问题并不能很好的缓解。

更详尽的反向传播推导：循环神经网络(RNN)的前向反向传播算法 - 刘建平Pinard

梯度裁剪

为了解决 RNN 因为循环层导致的梯度爆炸或消失问题，梯度裁剪（梯度截断）的方法被提了出来。

简单来说，梯度截断就是当梯度的模大于一定阈值时，就将它截断为一个比较小的数。即：

$\mathbf g\leftarrow\min\left(1,\frac\theta{||\mathbf g||}\right)\mathbf g$

式中， $\bf g$ 为梯度， $\theta$ 为给定阈值。

对于超参数 $\theta$ ，我们可以先进行数轮迭代，然后查看梯度范数的统计数据。以统计数据的均值作为 $\theta$ 的初始值是较为合理的初步尝试。

在 PyTorch 中内置了梯度裁剪方法：

torch.nn.utils.clip_grad_norm_(parameters, max_norm, norm_type=2)

# parameters：可迭代的网络参数
# max_norm：梯度范数的阈值/上限
# norm_type：范数类型

值得注意的是，在代码中每个批次的迭代过程如下：

  graph LR;
　　计算梯度-->梯度裁剪;
　　梯度裁剪-->更新参数;

因此， torch.nn.utils.clip_grad_norm_() 的使用应该在 loss.backward() 之后，optimizer.step() 之前。

除了梯度裁剪外，针对RNN还有时间步截断、随机截断等方法。但在实际工程中还是梯度裁剪更加普世且效果不错。

门控循环单元GRU

我们已经知道原始 RNN 具有长期依赖问题，因此产生了梯度消失或爆炸。
与之相关地，在实际工程中，有些情况下我们希望某些很重要的信息能够长久保留（即不更新隐状态）；而有些情况下我们希望某些没用的信息能够干脆别影响后续预测（即 重置隐状态）。

类比于电路原理中的“开关”，这两种策略的选择我们可以利用“门控”的方式进行抽象。并且，我们希望这种策略选择是可学习到的而不是人工调整的。

于是，采样这种思想设计的 RNN 就是门控循环单元（Gated Recurrent Unit，GRU），它是长短期记忆网络（Long-Short-Term Memory，LSTM） 的一个变种。GRU的计算速度更快，结构也相对简单，因此我们先介绍 GRU。

重置门与更新门

电路原理中的开关有高电平低电平之分，在数字电路中我们通常直接用 0 和 1 来表示开和关。类似地，GRU中的重置门（Reset Gate）和更新门（Update Gate）被设计为各元素大小处于 $(0,1)$ 区间中的向量，其中：

重置门 $\mathbf r_t$ 控制“可能还想记住”的过去状态的数量；
更新门 $\mathbf z_t$ 控制需要新状态中有多少个是旧状态的副本。

重置门和更新门的输入是由当前时间步的输入和前一时间步的隐状态给出。两个门的输出是由使用 $\text{Sigmoid}$ 激活函数（使输出为 $(0,1)$ ）的两个全连接层给出。

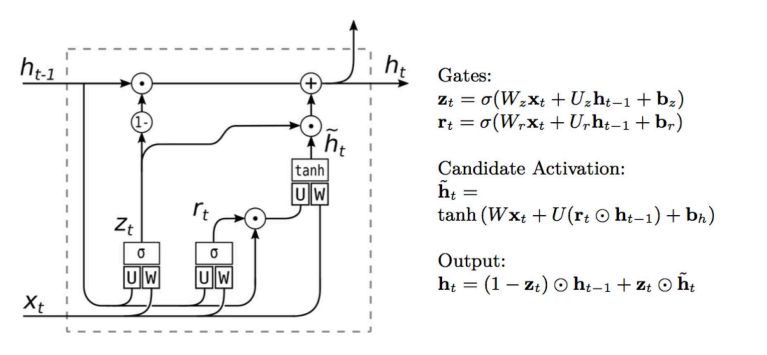
整个GRU的计算如下图所示：

候选隐状态

我们将重置门 $\mathbf r_t$ 与 RNN 中的常规隐状态更新机制集成，得到在时间步 $t$ 的候选隐状态（Candidate Hidden State） $\tilde{\mathbf h}_t$ 。

$\tilde{\mathbf h}_t=\tanh(W\mathbf x_t+U(\mathbf r_t\odot\mathbf h_{t-1})+\mathbf b_h)$

可见，当 ${\bf r}_t=\bf 0$ 时，该过程退化成了全连接层；当 ${\bf r}_t=\bf 1$ 时，该过程就变成了原始 RNN的隐藏层计算。所以，重置门控制了新状态中过去的隐状态信息应该保留多少。

GRU的隐状态

上述的计算结果只是候选隐状态，我们仍然需要结合更新门 $\mathbf z_t$ 来确定新的隐状态 $\mathbf h_t$ 在多大程度上来自旧的状态 $\mathbf h_{t-1}$ 和新的候选状态 $\tilde{\mathbf h}_t$ 。
事实上，更新门仅需要在状态之间进行按元素的凸组合就可以实现这个目标：

$\mathbf h_t=(1-\mathbf z_t)\odot\mathbf h_{t-1}+\mathbf z_t\odot\tilde{\mathbf h_t}$

可见，更新门控制了新状态中过去的隐状态本身被保留多少。当 ${\bf z}_t=\bf 0$ 时，模型就只保留旧状态，有效地跳过了长期依赖链条中的时间步。相反，当 ${\bf z}_t=\bf 1$ 时，新的隐状态就直接是候选隐状态。

这些设计可以帮助我们处理循环神经网络中的梯度消失问题，并更好地捕获时间步距离很长的序列的依赖关系。例如，如果整个子序列的所有时间步的更新门都接近于1，则无论序列的长度如何，在序列起始时间步的旧隐状态都将很容易保留并传递到序列结束。

更新门和重置门的公式是易于区分的，但它们的物理含义不易区分。
重置门是生成候选状态的时候这个状态蕴含了多少旧状态的信息；而更新门是生成当前时间步的隐状态时把多少旧状态的值保留下来。

总之，门控循环单元具有以下两个显著特征：

重置门有助于捕获序列中的短期依赖关系；
更新门有助于捕获序列中的长期依赖关系。

长短期记忆网络LSTM

长期以来，隐变量模型存在着长期信息保存和短期输入缺失的问题。解决这一问题的最早方法之一是长短期存储器（memory），它的设计比门控循环单元稍微复杂一些，但却比门控循环单元早诞生了近20年。

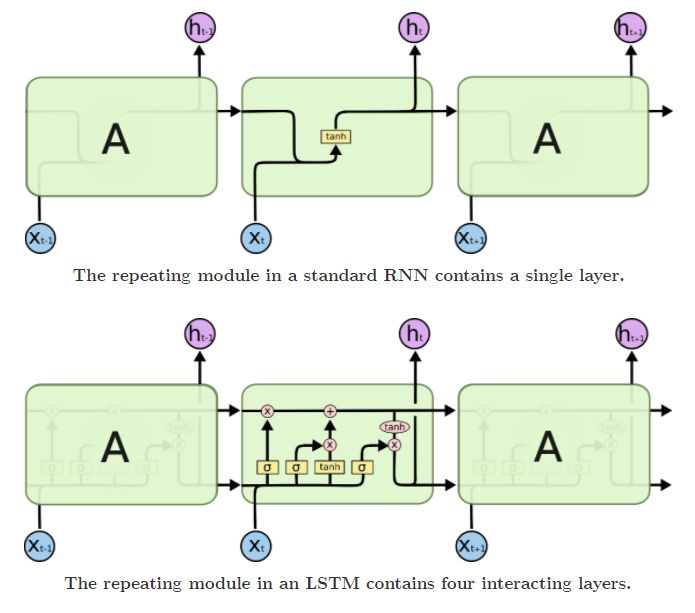
下面给出 RNN 与 LSTM 的结构图，LSTM每个环节我们再具体展开。

RNN与LSTM

记忆元

不难发现和 RNN 的前向传播相比，LSTM 在隐状态 $\bf h$ 之外还在网络中传递了另一种东西，记为 $C_t$ 。如下图所示。

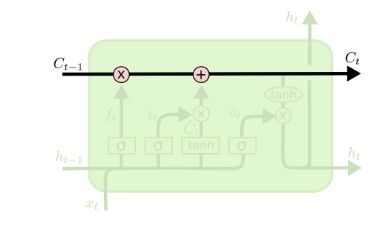
LSTM的记忆元

这个“东西”被称为记忆元（memory cell），或简称为细胞/单元（cell）。有些文献认为记忆元是隐状态的一种特殊类型，它们与隐状态具有相同的形状，其设计目的是用于记录附加的信息。

记忆元和隐状态一样都存储了上一时间步的信息，它的更新经过了下面这些门控结构的处理然后送到下一时间步，记忆元存储的信息也用于对隐状态进行更新。

门控结构

和 GRU 一样，LSTM 的门控结构也用于控制上一状态的信息保留情况，都通过 $\text{Sigmoid}$ 函数进行激活。主要由三个门控结构组成。分别是：遗忘门、输入门和输出门。

遗忘门（Forget Gate）顾名思义，是控制是否遗忘部分来自上一层的记忆元 $C_{t-1}$ 的信息；
输入门（Input Gate）负责将当前信息 $x_t$ 和上一层的隐状态 $h_{t-1}$ 输入给记忆元，以更新记忆元 $C_{t-1}\to C_t$ ；
输出门（Output Gate）自然就是确定输出隐状态 $h_t$ ，通过当前信息 $x_t$ 和上一层的隐状态 $h_{t-1}$ 以及更新得到的记忆元 $C_t$ 获得.

整体流程如下图所示：

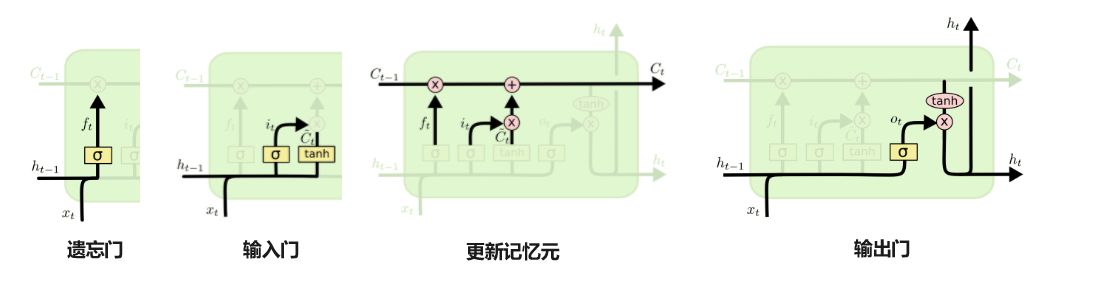
LSTM整体流程

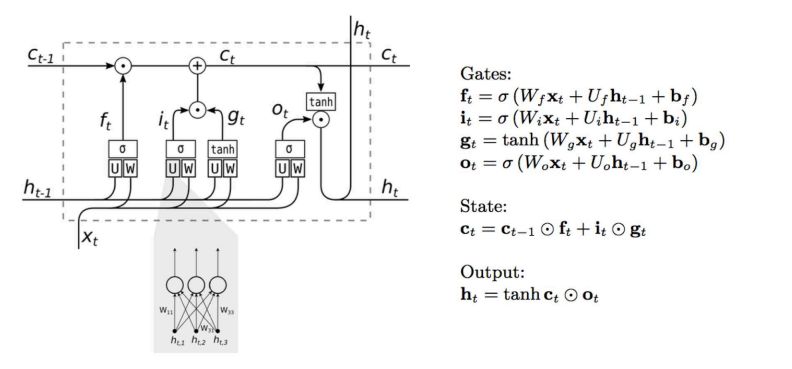
前向传播公式

上图给出了 LSTM 完整的前向传播。另外，LSTM 的反向传播推导可参考：循环神经网络(RNN)的前向反向传播算法 - 刘建平Pinard

RNN的变体

利用Concat

在前面我们讨论的 LSTM 和 GRU 中，其前向传播都是通过对 feature map 直接相加得来的。比如遗忘门：

$\mathbf f_t=\sigma(W_f\mathbf x_t+U_f\mathbf h_{t-1}+\mathbf b_f)$

事实上，也可以通过 feature map 进行拼接(Concat)，如：

$\mathbf f_t=\sigma([W_f\mathbf x_t\;||\;U_f\mathbf h_{t-1}]+\mathbf b_f')$

其中 $[\boldsymbol\alpha\;||\;\boldsymbol\beta]$ 表示将两个向量 $\boldsymbol\alpha,\boldsymbol\beta\in\Bbb R^n$ 拼接起来得到一个新的向量（ $\in\Bbb R^{2n}$ ）。

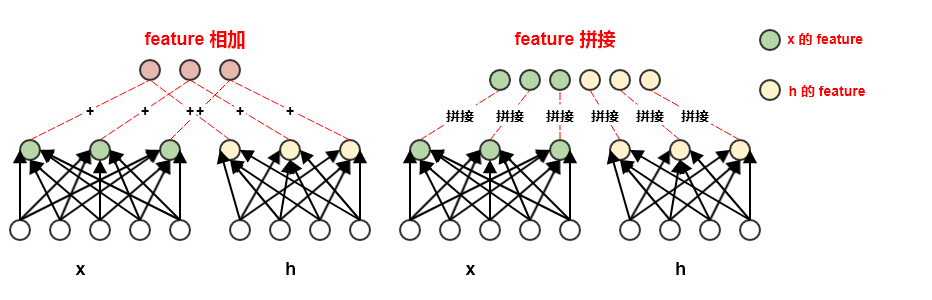
特征拼接vs特征相加

深度循环网络

为了应对更多问题，我们可以将多层循环神经网络堆叠在一起，通过对几个简单层的组合，产生了一个灵活的机制。

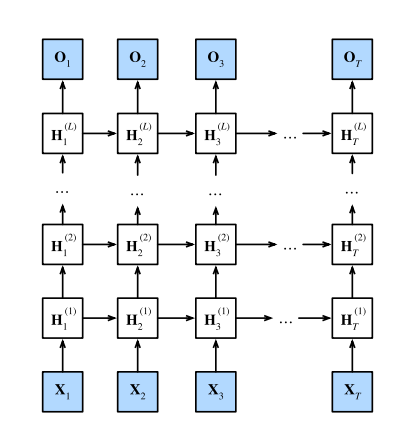
深度循环神经网络结构

其中，循环的网络层数 $L$ 和每层隐藏状态的维度都属于超参数。

双向循环网络

对于序列预测，我们还会遇见已知部分过去和未来的数据，然后预测当前情况的问题。
在数值分析上我们常见的有内插法这种方法，它通过过去和未来的数据来拟合出更好的曲线，从而确定当前的函数值。
但是若放在序列模型中，我们更希望用“外推法”来研究此类问题。

这类问题的输出可能依赖于整个输入序列。如：语音识别任务中，当前语音对应的单词不仅取决于前面的单词，也取决于后面的单词。因为词与词之间存在语义依赖。一个简单的示例如下：

1 2	Input: 这一切都是_____的选择！ Output：命运石之门

事实上，可能是收到了隐马尔可夫模型 的启迪，再加上简单的直觉，可以想象：只需要增加一个“从最后一个词元开始从后向前运行”的循环神经网络即可。

前向（forward）和后向（backward）两个RNN 得到的隐状态再连接起来共同作用于最后的输出，这样的结构就是双向循环神经网络（bidirectional RNNs）。经过实验表明，确实能够很好地应对上述问题。

一个以 LSTM 作为循环层的双向循环神经网络的结构如下图所示：

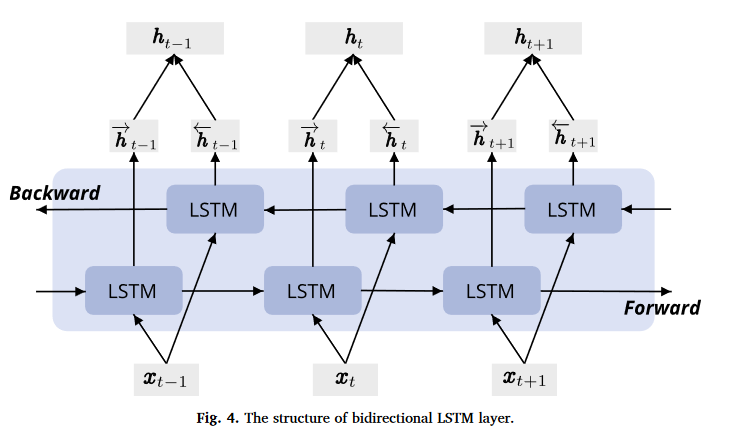
双向LSTM堆叠

这与隐马尔可夫模型中动态规划的前向和后向递归没有太大区别。其主要区别是，在隐马尔可夫模型中的方程具有特定的统计意义。双向循环神经网络没有这样容易理解的解释，我们只能把它们当作通用的、可学习的函数。
这种转变集中体现了现代深度网络的设计原则： 首先使用经典统计模型的函数依赖类型，然后将其参数化为通用形式。