本文内容涉及部分高等数学、线性代数、图数据结构的相关知识。如果有所遗忘或者想快速过一遍相关内容,可参阅本站文章:
Ax=λx 的几何意义
我们知道,一个n 维非零向量x∈Rn 可以由一个线性无关组(α1,α2,⋯,αn) 的线性组合进行表示,即:
x=k1α1+k2α2+⋯+knαn
我们称这个线性无关组是一组基,称(k1,k2,⋯,kn) 为向量x 在这组基下的坐标。
特别地,当这组基是单位正交向量组时,称其为规范正交基。
我们以最熟悉的笛卡尔坐标系为背景,对上述概念的几何意义做出解释。
假设存在一组二维的规范正交基(i,j) ,那么它们的任意线性组合就可以表示整个二维空间的所有向量。
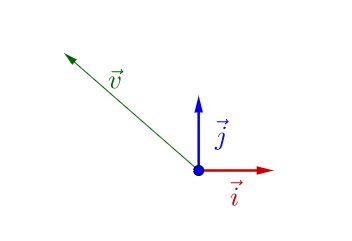
如上图所示,图中的向量v 可以由确定的坐标(a,b) 表示,也就是v=ai+bj.
除此之外,我们也学习过,向量左乘一个矩阵,可以看做是对其做线性变换,几何上相当于将一个向量进行旋转,平移等操作。
于是针对某个矩阵A,存在一系列在(i,j) 这组基下的向量x 和对应的实数λ 使得:
Ax=λx
也就是说,这些向量经过矩阵A 的变换之后,并不会旋转或者改变方向,只会在原有方向上进行比例为λ 的缩放。
我们称这样的向量x 为特征向量,λ 为特征值。(同一个A 可以有多个特征值和特征向量)从特征向量和特征值的定义式还可以看出,特征向量所在直线上的向量都是特征向量。
当然,我们可以计算得到某个矩阵的所有特征值,并给出一系列特征向量。(也有可能出行特征值是复数 complex number,不存在特征向量的情况,这种情况暂且不考虑)
并且,如果矩阵可以对角化,我们还可以进一步对其进行特征值分解:
A=PΛP−1=Pλ1λ2⋱λnP−1
其中,P 由A 的n 个线性无关的特征向量(正交)组成。
在几何意义上,我们知道A 包含了旋转与拉伸的作用。
而特征分解则分解出了用于旋转的P 和用于拉伸的Λ。
当我们把一幅图像视为一个矩阵,对其进行奇异值分解之后,对中间的对角阵进行处理:仅保留其最大的十几个特征值,其余元素置零。还原回去之后我们发现图像得到了压缩。
更多特征值分解已经奇异值分解的相关内容参阅本站文章:
拉普拉斯矩阵
拉普拉斯算子
拉普拉斯算子 Δf 是 n 维欧几里得空间中的一个二阶微分算子,定义为函数 f 的梯度 ∇f 的散度 ∇⋅∇f 。
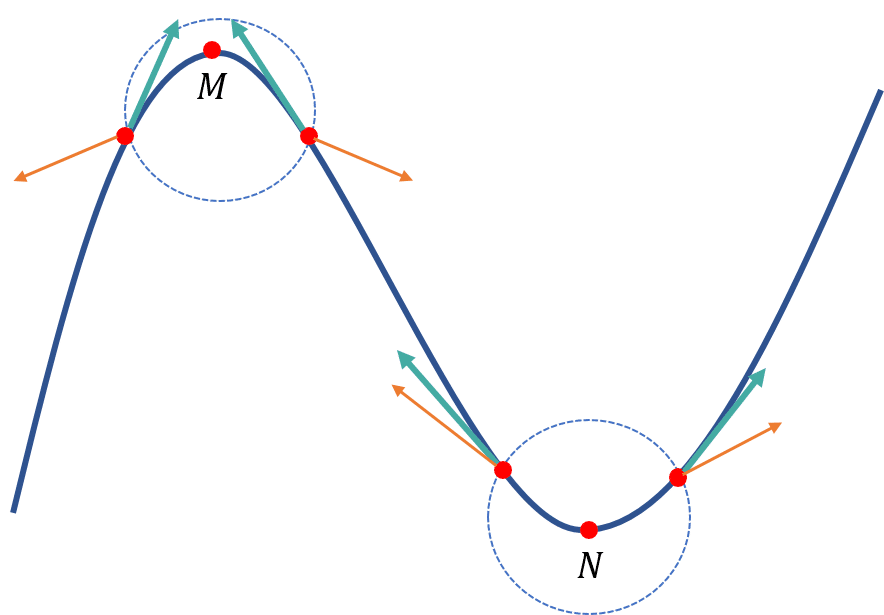
如上图所示,梯度表示某个点指向函数增加的方向(橙色箭头),而这些梯度构成了一个向量场(图中圆圈),梯度场的散度是对应点的法向量与梯度的点积之和。其中两个向量的夹角大于0时,其点积结果也大于0,反之则以。故梯度场的散度说明了极大值点和极小值点的汇聚和发散程度,系标量。
即,拉普拉斯算子衡量的是梯度场的发散程度。
二元函数Δf
我们可以容易写出二元函数f(x,y) 的拉普拉斯算子,其中二阶导数用差分近似。
比如对于二维图像来说,在(x,y) 处的像素值为f(x,y) ,则拉普拉斯算子如下:
∇2fwhere ∂x2∂2f∂y2∂2f∇2f=∂x2∂2f+∂y2∂2f≈f(x+1,y)+f(x−1,y)−2f(x,y)≈f(x,y+1)+f(x,y−1)−2f(x,y)=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)

如上图所示,其拉普拉斯算子也可以描述为与(x,y) 相邻点的像素值之和减去同次数的自身像素值。更形象的理解是,从该点出发沿着可能变化的四条路径,分别移动一步所获得的增益,这个增益实际上就是一种发散程度,或者说是净流入。
拉普拉斯矩阵推导
图结构的表示方式有两种:邻接表和邻接矩阵。本文重点关注图的邻接矩阵以便于谱图理论分析。
对于图G=(V,E) ,或有权图G=(V,E,W),每个节点的值由函数f 确定。
我们可以参照二元函数的离散版本拉普拉斯算子,对每个节点vi∈V 计算得到拉普拉斯算子:
Δf(vi)=vj∈N(vi)∑f(vj)−di⋅f(vi)
式中,N(vi) 表示节点vi 的邻接点集,di 表示节点vi 的度数,它等价于与该点相邻的节点个数。
考虑边权时(如果没有边,则权重记为0)还可以改写为:
Δf(vi)=j=1∑nwijf(vj)−di⋅f(vi)
记wi=[wi1,wi2,⋯,win],f=[f(v1),f(v2),⋯,f(vn)] ,则上式第一项可以写为wi⋅f.
更进一步地化简:
Δf=Δf(v1)Δf(v2)⋮Δf(vn)=w1⋅f−d1f(v1)w2⋅f−d2f(v2)⋮wn⋅f−dnf(vn)=W⋅f−d1d2⋱dnf=Wf−Df=(W−D)f
其中,W,D 分别是图G 的权重矩阵(不加权时,为邻接矩阵)和加权度矩阵(不加权时,为度数矩阵)。
经过以上推断,我们令L=D−W 为图G 的拉普拉斯矩阵。(注意相比上述推导多有一个负号)
L 的归一化
我们一般会对所得到的拉普拉斯矩阵进行归一化。
- 对称归一化:Lsym=I−D−1/2WD−1/2 .
- 其中D−1/2 是对元素而言,即[D−1/2]ii=1/dii
- 随机游走归一化:Lrw=I−D−1W
相关重要性质
拉普拉斯矩阵的二次型:
fTLf=21i=1∑nj=1∑nwij(fi−fj)2
- 显然fTLf≥0,故L 是半正定对称矩阵;
- 拉普拉斯矩阵的最小特征值为0,其对应的特征向量为全1常向量 1 ;
- 拉普拉斯矩阵有 n 个非负实数特征值,0=λ1≤λ2≤⋯≤λn;
- 假设 G 是一个有非负权重的无向图,其拉普拉斯矩阵 L 的特征值0的重数 k 等于图的联通分量的个数;
- 拉普拉斯矩阵的瑞利商处于[λ1,λn];
- 拉普拉斯矩阵可进行特征值分解:L=UΛUT,其中Λ=diag(λi) ,U 由其n个线性无关的单位正交特征向量组成。
物理含义
将拉普拉斯矩阵绘制成图像可以得到“拉普拉斯图”。
从图中直观地显示了当我们在某节点中放置一些 “潜在元素” 时,“能量” 在图上的传播方向和扩散程度。
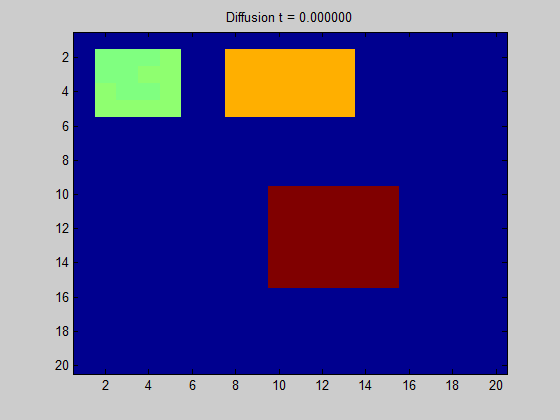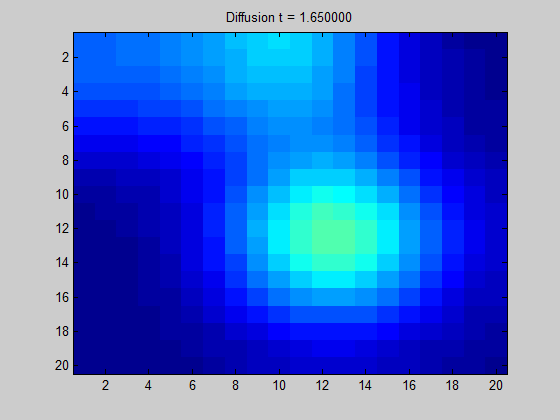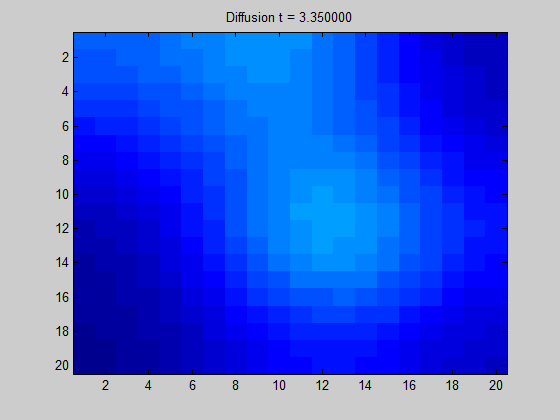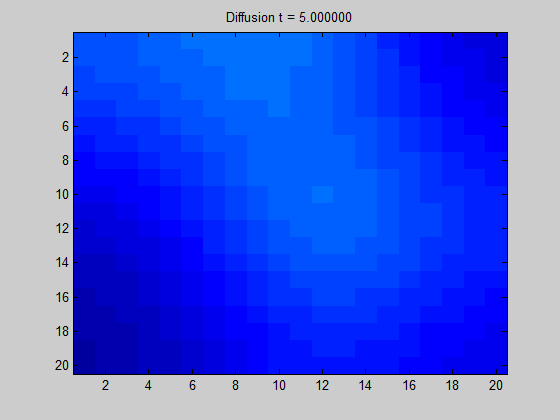
特征向量制图
低频特征值(除了λ1=0 外的较小几个特征值)所对应的特征向量可用于图结构模拟。
特别地,对于一个 k 维空间的柏拉图立体(即正多面体),将其拉普拉斯矩阵的第 2 至 k+1 个特征值所对应的特征向量(即ψ2,ψ3,…,ψk+1)作为对应坐标系的坐标,即可得到该图结构的模拟。(读书报告 | 谱图理论 Ch3: The Laplacian and Graph Drawing - 知乎 (zhihu.com))
图傅里叶变换
传统傅里叶变换告诉了我们以下知识:
➢傅里叶反变换:把任意一个函数表示成了若干正交基函数的线性组合。
➢傅里叶正变换:求线性组合系数。具体做法是由原函数和基的 共轭的内积 求得。
对应图上的信号f∈Rn,如果要进行傅里叶变换,很自然的我们能想到:我们也要找到一组正交基,通过这组正交基的线性组合来表达f .
事实上,经典傅里叶变换的基函数是拉普拉斯算子的特征函数。(算子在指定一个点的计算结果是一个数值,所以对应有特征值;而算子用特定函数表示时,就对应有特征函数)
所以图傅里叶变换则是将拉普拉斯矩阵的特征向量作为图傅里叶变换的基函数。
于是有:
f=f^(λ1)ψ1+f^(λ2)ψ2+⋯+f^(λn)ψn
这就是图中的傅里叶逆变换。
因为这n 个特征向量ψi 组成L=UΛUT 中的U。所以上式也可以写为:
f=Uf^,f^=[f^(λ2),f^(λ2),...,f^(λn)]T
而f^ 就是谱域/频域中的信号,它的自变量为n 个特征值。
不难得出,还有f^=UTf,这是图中的傅里叶正变换。
图谱上的卷积
类比经典傅里叶变换的性质:时域上的卷积结果等于频域上的乘积再反变换回来。
我们得到图在空域上的卷积就等于图在谱域中的乘积再逆变换。所以有:
f∗g=F−1(f^⊙g^)=U(UTg⊙UTf)
如果令gθ(Λ)=diag(g^)=diag(UTg),则UTg⊙UTf 就可以写成gθ(Λ)UTf,所以:
f∗g=Ugθ(Λ)UTf
在工程应用中,我们还可以利用切比雪夫最佳逼近多项式来进一步对卷积操作进行计算优化。关于这一点可以参考本站文章:图网络浅学:图神经网络及其发展 - GNN
参考
- 如何理解矩阵特征值和特征向量?- 马同学
- 读书报告 | 谱图理论 Ch1: Introduction - 知乎
- 机器学习 - 拉普拉斯算子 与 拉普拉斯矩阵
- 谱图理论(spectral graph theory)-CSDN博客
- 读书报告 | 谱图理论 Ch3: The Laplacian and Graph Drawing - 知乎
- 图卷积神经网络笔记——第二章:谱域图卷积介绍(1)-CSDN博客
- 理解图傅里叶变换,图卷积,基于频域的图卷积神经网络 (GCN) - 知乎